Chỉ ra hai đường thẳng cắt nhau và song song với \(\left( {BA’C’} \right)\). Hướng dẫn trả lời Giải bài 40 trang 113 sách bài tập toán 11 – Cánh diều – Bài 5. Hình lăng trụ và hình hộp. Cho hình hộp \(ABCD.A’B’C’D’\)….
Đề bài/câu hỏi:
Cho hình hộp \(ABCD.A’B’C’D’\). Mặt phẳng \(\left( {BA’C’} \right)\) song song với mặt phẳng nào dưới đây?
A. \(\left( {ACD} \right)\)
B. \(\left( {ADD’} \right)\)
C. \(\left( {DCD’} \right)\)
D. \(\left( {AD’C} \right)\)
Hướng dẫn:
Chỉ ra hai đường thẳng cắt nhau và song song với \(\left( {BA’C’} \right)\), mặt phẳng chứa hai đường thẳng đó là mặt phẳng cần tìm.
Lời giải:
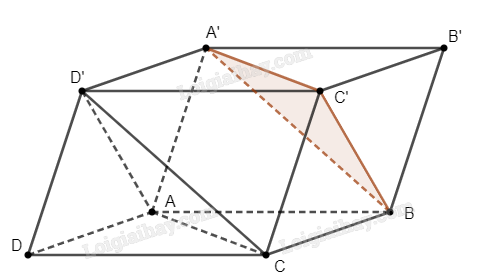
Do hình hộp là hình lăng trụ, các mặt bên là hình bình hành nên ta có \(ADD’A’\) và \(DCC’D’\) là các hình bình hành.
Ta có \(A’ \in \left( {ADD’A’} \right) \cap \left( {BA’C’} \right)\) nên hai mặt phẳng \(\left( {ADD’A’} \right)\) và \(\left( {BA’C’} \right)\) có điểm chung, tức là chúng không song song với nhau.
Chứng minh tương tự, hai mặt phẳng \(\left( {BA’C’} \right)\) và \(\left( {DCD’} \right)\) không song song với nhau, và hai mặt phẳng \(\left( {BA’C’} \right)\) và \(\left( {ACD} \right)\) cũng không song song với nhau.
Nhận xét rằng tứ giác \(ACC’A’\) có \(AA’ = CC’\) và \(AA’\parallel CC’\) nên nó là hình bình hành. Suy ra \(A’C’\parallel AC\). Do \(AC \subset \left( {AD’C} \right)\) nên \(A’C’\parallel \left( {AD’C} \right)\).
Chứng minh tương tự ta cũng có \(BC’\parallel \left( {AD’C} \right)\). Như vậy \(\left( {BA’C’} \right)\parallel \left( {AD’C} \right)\).
Đáp án đúng D.