Để chứng minh 2 mặt phẳng vuông góc, ta cần chứng minh 1 đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng. Giải chi tiết Giải bài 39 trang 104 sách bài tập toán 11 – Cánh diều – Bài 4. Hai mặt phẳng vuông góc. Cho hình lăng trụ \(ABC.A’B’C’\) có \(AA’ \bot \left( {ABC} \right)\…
Đề bài/câu hỏi:
Cho hình lăng trụ \(ABC.A’B’C’\) có \(AA’ \bot \left( {ABC} \right)\), tam giác \(ABC\) cân tại \(A\). Gọi \(M\) là trung điểm của \(BC\). Chứng minh rằng \(\left( {MAA’} \right) \bot \left( {BCC’B’} \right)\).
Hướng dẫn:
Để chứng minh 2 mặt phẳng vuông góc, ta cần chứng minh 1 đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
Lời giải:
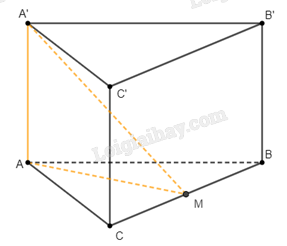
Vì tam giác \(ABC\) cân tại \(A\), \(M\) là trung điểm của \(BC\) nên \(AM \bot BC\).
Do \(AA’ \bot \left( {ABC} \right)\), ta suy ra \(BB’ \bot \left( {ABC} \right)\). Điều này dẫn tới \(BB’ \bot AM\).
Như vậy, do \(AM \bot BC\), \(BB’ \bot AM\), ta suy ra \(AM \bot \left( {BCC’B’} \right)\).
Mà \(AM \subset \left( {MAA’} \right)\), nên \(\left( {MAA’} \right) \bot \left( {BCC’B’} \right)\).
Bài toán được chứng minh.