Giả sử có ba mặt phẳng \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) thoả mãn \(\left( P \right)\parallel \left( Q \right)\. Trả lời Giải bài 38 trang 104 sách bài tập toán 11 – Cánh diều – Bài 4. Hai mặt phẳng vuông góc. Chứng minh các định lí sau:…
Đề bài/câu hỏi:
Chứng minh các định lí sau:
a) Cho hai mặt phẳng song song. Nếu một mặt phẳng vuông góc với một trong hai mặt phẳng đó thì vuông góc với mặt phẳng còn lại.
b) Cho một mặt phẳng và một đường thẳng không vuông góc với mặt phẳng đó. Khi đó tồn tại duy nhất một mặt phẳng chứa đường thẳng đã cho và vuông góc với mặt phẳng đã cho.
Hướng dẫn:
a) Giả sử có ba mặt phẳng \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) thoả mãn \(\left( P \right)\parallel \left( Q \right)\) và \(\left( P \right) \bot \left( R \right)\). Ta cần chứng minh \(\left( Q \right) \bot \left( R \right)\).
b) Xét đường thẳng \(d\) không vuông góc với mặt phẳng \(\left( P \right)\). Chỉ ra rằng tồn tại duy nhất mặt phẳng \(\left( Q \right)\) vuông góc với \(\left( P \right)\) và chứa \(d\).
Lời giải:
a)
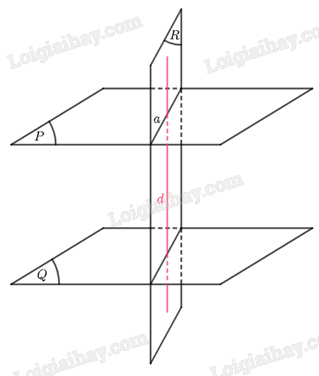
Giả sử có ba mặt phẳng \(\left( P \right)\), \(\left( Q \right)\), \(\left( R \right)\) thoả mãn \(\left( P \right)\parallel \left( Q \right)\) và \(\left( P \right) \bot \left( R \right)\). Ta cần chứng minh \(\left( Q \right) \bot \left( R \right)\). Thật vậy, gọi \(a\) là giao tuyến của \(\left( P \right)\) và \(\left( R \right)\). Lấy đường thẳng \(d\) nằm trong \(\left( R \right)\) sao cho \(a \bot d\).
Vì \(\left( P \right) \bot \left( R \right)\), \(a = \left( P \right) \cap \left( R \right)\), \(a \bot d\), ta suy ra \(d \bot \left( P \right)\).
Mà \(\left( P \right)\parallel \left( Q \right)\), ta có \(d \bot \left( Q \right)\). Do \(d \subset \left( R \right)\) nên ta suy ra \(\left( Q \right) \bot \left( R \right)\). Bài toán được chứng minh.
b) Xét đường thẳng \(d\) không vuông góc với mặt phẳng \(\left( P \right)\). Chỉ ra rằng tồn tại duy nhất mặt phẳng \(\left( Q \right)\) vuông góc với \(\left( P \right)\) và chứa \(d\).
Xét trường hợp \(d\) cắt \(\left( P \right)\) tại \(A\). (Các trường hợp \(d \subset \left( P \right)\) và \(d\parallel \left( P \right)\) chứng minh tương tự).
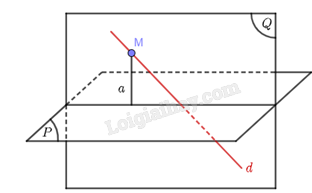
Lấy \(M \in d\) sao cho \(M \ne A\). Vẽ đường thẳng \(a\) đi qua \(M\) sao cho \(a \bot \left( P \right)\). Ta nhận xét rằng \(a\) và \(d\) cắt nhau, nên mặt phẳng \(\left( Q \right)\) chứa hai đường thẳng \(a\) và \(d\).
Vì \(a \bot \left( P \right)\), \(a \subset \left( Q \right)\) nên ta suy ra \(\left( P \right) \bot \left( Q \right)\).
Giả sử tồn tại mặt phẳng \(\left( {Q’} \right)\) sao cho \(\left( P \right) \bot \left( {Q’} \right)\) và \(d \subset \left( {Q’} \right)\). Ta thấy rằng \(d\) là giao tuyến của \(\left( {Q’} \right)\) và \(\left( Q \right)\). Do \(\left( P \right) \bot \left( Q \right)\) và \(\left( P \right) \bot \left( {Q’} \right)\), ta suy ra \(d \bot \left( P \right)\). Điều này là vô lí, vì \(d\) không vuông góc với \(\left( P \right)\). Như vậy, \(\left( Q \right)\) là duy nhất.
Bài toán được chứng minh.