Gọi \(P\) là hình chiếu của \(A\) trên \(SO\). Trên \(\left( {SAC} \right)\), gọi \(M\) là giao điểm của \(SC\) và \(AP\). Hướng dẫn cách giải/trả lời Giải bài 30 trang 100 sách bài tập toán 11 – Cánh diều – Bài 3. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện. Cho hình chóp \(S.ABCD\) có \(AC\) cắt \(BD\) tại \(O\)….
Đề bài/câu hỏi:
Cho hình chóp \(S.ABCD\) có \(AC\) cắt \(BD\) tại \(O\). Gọi \(\alpha \), \(\beta \) lần lượt là số đo của các góc nhị diện \(\left[ {A,SO,B} \right]\) và \(\left[ {B,SO,C} \right]\). Tính \(\alpha + \beta \).
Hướng dẫn:
Gọi \(P\) là hình chiếu của \(A\) trên \(SO\). Trên \(\left( {SAC} \right)\), gọi \(M\) là giao điểm của \(SC\) và \(AP\). Trên \(\left( {SBD} \right)\), kẻ \(NP \bot SO\) với \(N \in SB\). Chứng minh được \(\widehat {APN}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,B} \right]\) và \(\widehat {NPM}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SO,C} \right]\), từ đó tính được \(\alpha + \beta \).
Lời giải:
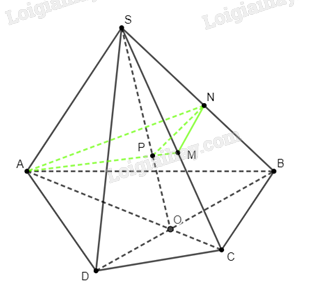
Gọi \(P\) là hình chiếu của \(A\) trên \(SO\). Trên \(\left( {SAC} \right)\), gọi \(M\) là giao điểm của \(SC\) và \(AP\). Trên \(\left( {SBD} \right)\), kẻ \(NP \bot SO\) với \(N \in SB\).
Dễ thấy rằng 4 điểm \(A\), \(P\), \(M\), \(N\) đồng phẳng.
Vì \(AP \bot SO\), \(NP \bot SO\) nên góc \(\widehat {APN}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SO,B} \right]\), tức là \(\alpha = \widehat {APN}\).
Chứng minh tương tự, ta có \(\beta = \widehat {NPM}\)
Suy ra \(\alpha + \beta = \widehat {APN} + \widehat {NPM} = \widehat {APM}\). Mặt khác, do \(A\), \(P\), \(M\) thẳng hàng, nên ta có \(\widehat {APM} = {180^o}\).
Như vậy \(\alpha + \beta = {180^o}\).