Bài 14 trang 95 SBT toán 11 – Cánh diều: Cho hình hộp ABCD. A’B’C’D’ có ABCD là hình thoi, AA’ ⊥ ABCD . Chứng minh rằng: a) BB’ ⊥ A’B’C’D’ ; b) BD ⊥ A’C.

Đề bài/câu hỏi:

Cho hình hộp ABCD.A’B’C’D’ có ABCD là hình thoi, \(AA’ \bot \left( {ABCD} \right).\)Chứng minh rằng:

a) \(BB’ \bot \left( {A’B’C’D’} \right);\)

b) \(BD \bot A’C.\)

Hướng dẫn:

Sử dụng định lý ba đường vuông góc.

Lời giải:

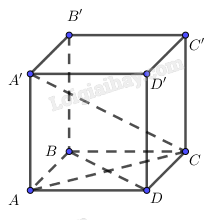
a) Vì ABCD.A’B’C’D’ là hình hộp nên \(AA'{\rm{ // }}BB’.\) Mà \(AA’ \bot \left( {ABCD} \right)\) nên \(BB’ \bot \left( {ABCD} \right).\) Mặt khác \(\left( {ABCD} \right){\rm{ // }}\left( {A’B’C’D’} \right) \Rightarrow BB’ \bot \left( {A’B’C’D’} \right).\)

b) Vì ABCD là hình thoi nên \(AC \bot BD.\) Do \(AA’ \bot \left( {ABCD} \right)\) nên AC là hình chiếu của \(A’C\) trên mặt phẳng (ABCD). Theo định lí ba đường vuông góc suy ra \(BD \bot A’C.\)