Hướng dẫn giải Luyện tập 2 Bài 4. Phép quay và phép đối xứng tâm (trang 17, 18) – Chuyên đề học tập Toán 11 Kết nối tri thức. Gợi ý: Phép quay tâm O, góc quay.
Câu hỏi/Đề bài:
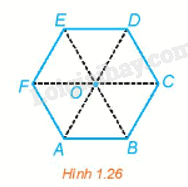
Trong Hình 1.26, ABCDEF là lục giác đều có tâm O. Tìm ảnh của tam giác ACE qua các phép quay \({Q_{\left( {O,\,\frac{\pi }{3}} \right)}},\,\,{Q_{\left( {O,\, – \frac{{2\pi }}{3}} \right)}}\)
Hướng dẫn:
Phép quay tâm O, góc quay :
Khi đó, \(\left\{ \begin{array}{l}x’ = x\cos \alpha – y\sin \alpha \\y’ = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Lời giải:
Ta có: ABCDEF là lục giác đều nên
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = 60^\circ = \frac{\pi }{3}\) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC{\rm{ }} = {\rm{ }}OD{\rm{ }} = {\rm{ }}OE{\rm{ }} = {\rm{ }}OF\).
Do đó, phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến các điểm A, C, E tương ứng thành các điểm B, D, F.
Vậy phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến tam giác ACE thành tam giác BDF.
Ta có: \(\widehat {AOE} = \widehat {AOF} + \widehat {EOF} = \frac{{2\pi }}{3}\), tương tự \(\widehat {COA} = \widehat {EOC} = \frac{{2\pi }}{3}\)
Vì OA = OE và góc quay \( – \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, – \frac{{2\pi }}{3}} \right)}}\) biến điểm A thành điểm E.
Vì OC = OA và góc quay \( – \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, – \frac{{2\pi }}{3}} \right)}}\) biến điểm C thành điểm A.
Vì OE = OC và góc quay \( – \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, – \frac{{2\pi }}{3}} \right)}}\) biến điểm E thành điểm C.
Vậy phép quay \({Q_{\left( {O,\, – \frac{{2\pi }}{3}} \right)}}\) biến tam giác ACE thành tam giác ECA hay biến tam giác ACE thành chính nó.