Ta cần tìm tâm và góc quay: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phân tích, đưa ra lời giải Giải bài 1.11 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức – Bài 4. Phép quay và phép đối xứng tâm – Chuyên đề học tập Toán 11 Kết nối tri thức. Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A….
Đề bài/câu hỏi:
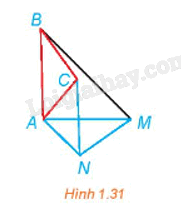
Trong Hình 1.31, BAM và CAN là các tam giác vuông cân tại A. Hãy chỉ ra một phép quay biến tam giác ABC thành tam giác AMN.
Hướng dẫn:
Ta cần tìm tâm và góc quay: Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM’\) và góc lượng giác \(\left( {OM,OM’} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải:
Tam giác BAM vuông cân tại A nên AB = AM và \(\widehat {BAM} = 90^\circ \). Do đó, ta có phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến điểm A thành điểm A, biến điểm B thành điểm M (1).
Tam giác ACN vuông cân tại A nên AC = AN và \(\widehat {CAN} = 90^\circ \). Do đó, ta có phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến điểm C thành điểm N (2).
Từ (1) và (2) suy ra phép quay \({Q_{(A,{\rm{ }}-{\rm{ }}90^\circ )}}\) biến tam giác ABC thành tam giác AMN.