Một đồ thị không có khuyên, trong đó hai đỉnh được nối bằng nhiều nhất một cạnh (không có hai cạnh nào cùng nối một. Trả lời Giải bài 2.20 trang 50 Chuyên đề học tập Toán 11 Kết nối tri thức – Bài tập cuối chuyên đề 2 – Chuyên đề học tập Toán 11 Kết nối tri thức. Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau:…
Đề bài/câu hỏi:
Vẽ đồ thị G = (V, E) với các đỉnh và các cạnh như sau:
V = {1; 2; 3; 4; 5; 6; 7; 8} và E = {12; 13; 23; 34; 35; 67; 68; 78}.
Đồ thị này có phải là đơn đồ thị không? Có phải là đồ thị đầy đủ không?
Hướng dẫn:
– Một đồ thị không có khuyên, trong đó hai đỉnh được nối bằng nhiều nhất một cạnh (không có hai cạnh nào cùng nối một cặp đỉnh) gọi là một đơn đồ thị.
– Một đồ thị là đầy đủ khi và chỉ khi mỗi cặp đỉnh của nó đều được nối bằng một cạnh.
Lời giải:
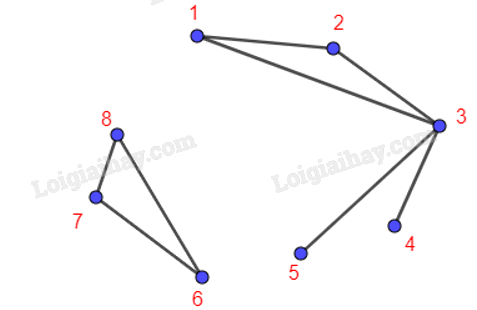
Ta vẽ được đồ thị G như hình trên.
Đồ thị G này không có khuyên và hai đỉnh chỉ được nối với nhau bằng nhiều nhất một cạnh nên là một đơn đồ thị.
Đồ thị G không phải đồ thị đầy đủ vì không phải tất cả các cặp đỉnh của nó đều được nối với nhau bằng một cạnh.