Vận dụng 2 Bài 6 (trang 32, 33, 34, 35) Chuyên đề học tập Toán 11: Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự V_O, – 1/2

Câu hỏi/Đề bài:

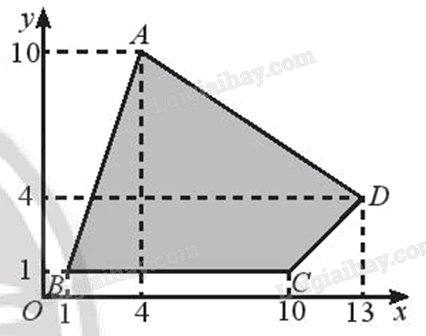
Vẽ Hình 11 ra giấy kẻ ô li và tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, – \frac{1}{2}} \right)}}\).

Hướng dẫn:

Để tìm ảnh của tứ giác ABCD qua phép vị tự \({V_{\left( {O, – \frac{1}{2}} \right)}}\) ta tìm ảnh của từng điểm A, B, C, D qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\). Sau đó nối chúng lại với nhau.

Lời giải:

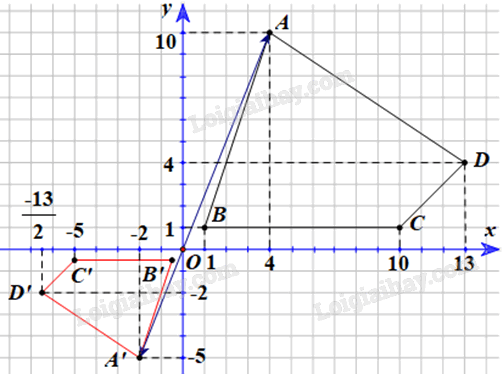
Để tìm ảnh của tứ giác ABCD qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\), ta tìm ảnh của các điểm A, B, C, D qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\).

Quan sát hình vẽ, ta thấy \(\;A\left( {4;{\rm{ }}10} \right),{\rm{ }}B\left( {1;{\rm{ }}1} \right),{\rm{ }}C\left( {10;{\rm{ }}1} \right),{\rm{ }}D\left( {13;{\rm{ }}4} \right).\)

⦁ Đặt là ảnh của A qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\)

Suy ra \(\overrightarrow {O{A’}} = – \frac{1}{2}\overrightarrow {OA} \) với \(\overrightarrow {OA} = \left( {4;10} \right)\) và \(\overrightarrow {O{A’}} = \left( {{x_{A’}};{y_{A’}}} \right)\)

Do đó \(\left\{ \begin{array}{l}{x_{A’}} = – \frac{1}{2}.4 = – 2\\{y_{A’}} = – \frac{1}{2}.10 = – 5\end{array} \right.\)

Vì vậy tọa độ

⦁ Đặt \(B’\left( {{x_{B’}};{y_{B’}}} \right)\) là ảnh của B qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\)

Suy ra \(\overrightarrow {O{B’}} = – \frac{1}{2}\overrightarrow {OB} \) với \(\overrightarrow {OB} = \left( {1;1} \right)\) và \(\overrightarrow {O{B’}} = \left( {{x_{B’}};{y_{B’}}} \right)\)

Do đó \(\left\{ \begin{array}{l}{x_{B’}} = – \frac{1}{2}.1 = – \frac{1}{2}\\{y_{B’}} = – \frac{1}{2}.1 = – \frac{1}{2}\end{array} \right.\)

Vì vậy tọa độ \(B’\left( { – \frac{1}{2}; – \frac{1}{2}} \right)\)

⦁ Đặt \(C’\left( {{x_{C’}};{y_{C’}}} \right)\) là ảnh của C qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\)

Suy ra \(\overrightarrow {OC’} = – \frac{1}{2}\overrightarrow {OC} \) với \(\overrightarrow {OC} = \left( {10;1} \right)\) và \(\overrightarrow {OC’} = \left( {{x_{C’}};{y_{C’}}} \right)\)

Do đó \(\left\{ \begin{array}{l}{x_{C’}} = – \frac{1}{2}.10 = – 5\\{y_{C’}} = – \frac{1}{2}.1 = – \frac{1}{2}\end{array} \right.\)

Vì vậy tọa độ \(C’\left( { – 5; – \frac{1}{2}} \right)\)

⦁ Đặt \(D’ = \left( {{x_{D’}};{y_{D’}}} \right)\) là ảnh của D qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\)

Suy ra \(\overrightarrow {OD’} = – \frac{1}{2}\overrightarrow {OD} \)với \(\overrightarrow {OD} = \left( {13;4} \right)\) và \(\overrightarrow {O{D’}} = \left( {{x_{D’}};{y_{D’}}} \right)\)

Do đó \(\left\{ \begin{array}{l}{x_{D’}} = – \frac{1}{2}.13 = – \frac{{13}}{2}\\{y_{D’}} = – \frac{1}{2}.4 = – 2\end{array} \right.\)

Vì vậy tọa độ \(D’\left( { – \frac{{13}}{2}; – 2} \right)\)

Vậy ảnh của tứ giác ABCD qua \({V_{\left( {O, – \frac{1}{2}} \right)}}\) là tứ giác A’B’C’D’ có tọa độ các đỉnh là \(A’\left( {-2;{\rm{ }}-5} \right),B’\left( { – \frac{1}{2}; – \frac{1}{2}} \right),C’\left( { – 5; – \frac{1}{2}} \right),D’\left( { – \frac{{13}}{2}; – 2} \right)\)