Đáp án Khám phá 4 Bài 6. Phép vị tự (trang 32, 33, 34, 35) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Gợi ý: Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|.
Câu hỏi/Đề bài:
Cho phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}\) và đường tròn (C) tâm I bán kính r. Xét điểm M thuộc (C), gọi I’ và M’ là ảnh của I và M qua phép vị tự \({V_{\left( {O,{\rm{ }}k} \right)}}.\)
a) Tính I’M’ theo r và k.
b) Khi cho điểm M chạy trên đường tròn (C) thì M’ chạy trên đường nào?
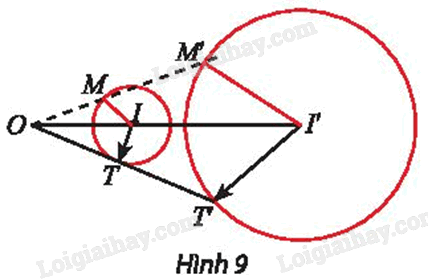
Hướng dẫn:
Phép vị tự tỉ số k biến đoạn thẳng thành đoạn thẳng nhân lên với |k|, biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng |k|, biến đường tròn bán kính r thành đường tròn bán kính \(r’ = |k|.r\).
Lời giải:
a) Ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\left( I \right){\rm{ }} = {\rm{ }}I’\) và \({V_{\left( {O,{\rm{ }}k} \right)}}\left( M \right){\rm{ }} = {\rm{ }}M’.\)
Suy ra \(I’M'{\rm{ }} = {\rm{ }}\left| k \right|.IM{\rm{ }} = {\rm{ }}\left| k \right|.r.\)
Vậy
b) Theo đề, ta có \({V_{\left( {O,{\rm{ }}k} \right)}}\;\) biến điểm M thành điểm M’.
Vậy khi M chạy trên đường tròn (C) thì M’ chạy trên đường tròn (C’) có tâm I’, bán kính \(r'{\rm{ }} = {\rm{ }}\left| k \right|.r\) là ảnh của (C) qua \({V_{\left( {O,{\rm{ }}k} \right)}}.\)