Đáp án Khám phá 3 Bài 6. Phép vị tự (trang 32, 33, 34, 35) – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Gợi ý: Chứng minh hai vectơ \(\overrightarrow {B’A’} \) và \(m\overrightarrow {B’C’} \) cùng bằng vectơ thứ ba.
Câu hỏi/Đề bài:
Gọi A’, B’ và C’ lần lượt là ảnh của ba điểm thẳng hàng A, B, C qua phép vị tự \({V_{(O,{\rm{ }}k)}}.\) Cho biết \(\overrightarrow {BA} = m\overrightarrow {BC} \) hai vectơ \(\overrightarrow {B’A’} \) và \(m\overrightarrow {B’C’} \) có bằng nhau không?
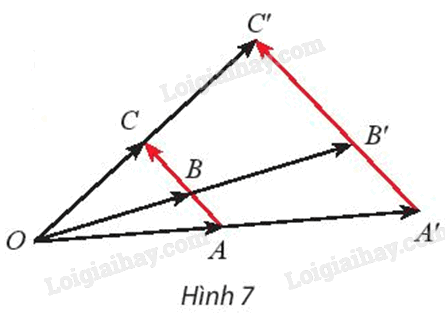
Hướng dẫn:
Chứng minh hai vectơ \(\overrightarrow {B’A’} \) và \(m\overrightarrow {B’C’} \) cùng bằng vectơ thứ ba.
Lời giải:
Theo bài, ta có A’, B’ lần lượt là ảnh của A, B qua \({V_{(O,{\rm{ }}k)}}.\)
Áp dụng tính chất 1, ta được \(\overrightarrow {B’A’} = k\overrightarrow {BA} \)
Chứng minh tương tự, ta được \(\overrightarrow {B’C’} = k\overrightarrow {BC} \)
Ta có \(\overrightarrow {B’A’} = k\overrightarrow {BA} = k.m\overrightarrow {BC} = m.k\overrightarrow {BC} = m\overrightarrow {B’C’} \)
Vậy hai vectơ \(\overrightarrow {B’A’} \) và \(m\overrightarrow {B’C’} \) bằng nhau.