Nếu mỗi cạnh của đồ thị G được gắn với một số thực (có thể là độ dài của đường đi trên mỗi cạnh. Trả lời Giải bài 1 trang 66 Chuyên đề học tập Toán 11 Chân trời sáng tạo – Bài 3. Bài toán tìm đường đi ngắn nhất – Chuyên đề học tập Toán 11 Chân trời sáng tạo. Cho đồ thị có trọng số như Hình 16….
Đề bài/câu hỏi:
Cho đồ thị có trọng số như Hình 16.
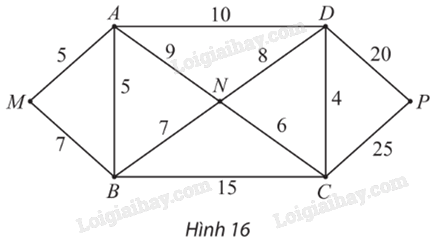
a) Tính độ dài các đường đi ABCD, MBNCP.
b) Chỉ ra ba đường đi khác nhau từ M đến N và tính độ dài của chúng.
c) MBC có phải là đường đi ngắn nhất từ M đến C không?
Hướng dẫn:
Nếu mỗi cạnh của đồ thị G được gắn với một số thực (có thể là độ dài của đường đi trên mỗi cạnh, chi phí vận chuyển trên mỗi cạnh đó,…) thì đồ thị G được gọi là đồ thị có trọng số. Trọng số của cạnh a kí hiệu là \({w_a}\)
Tổng trọng số (hay độ dài) của các cạnh tạo thành đường đi gọi là độ dài của đường đi đó. Độ dài đường đi m kí hiệu là \({l_m}\). Đường đi có độ dài ngắn nhất trong các đường đi từ đỉnh A đến đỉnh B gọi là đường đi ngắn nhất từ A đến B.
Lời giải:
a) Ta có:
\(\begin{array}{*{20}{l}}{{l_{ABCD}}\; = {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BC}}\; + {\rm{ }}{w_{CD}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}15{\rm{ }} + {\rm{ }}4{\rm{ }} = {\rm{ }}24.}\\{{l_{MBNCP}}\; = {\rm{ }}{w_{MB}}\; + {\rm{ }}{w_{BN}}\; + {\rm{ }}{w_{NC}}\; + {\rm{ }}{w_{CP}}\; = {\rm{ }}7{\rm{ }} + {\rm{ }}7{\rm{ }} + {\rm{ }}6{\rm{ }} + {\rm{ }}25{\rm{ }} = {\rm{ }}45.}\end{array}\)
Vậy độ dài các đường đi ABCD, MBNCP lần lượt là 24 và 45.
b) Ba đường đi khác nhau từ M đến N là: MAN, MBN, MABN.
Ta có:
\(\begin{array}{*{20}{l}}{{l_{MAN}}\; = {\rm{ }}{w_{MA}}\; + {\rm{ }}{w_{AN}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}9{\rm{ }} = {\rm{ }}14.}\\{{l_{MBN}}\; = {\rm{ }}{w_{MB}}\; + {\rm{ }}{w_{BN}}\; = {\rm{ }}7{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}14.}\\{{l_{MABN}}\; = {\rm{ }}{w_{MA}}\; + {\rm{ }}{w_{AB}}\; + {\rm{ }}{w_{BN}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}5{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}17.}\end{array}\)
Vậy ba đường đi khác nhau từ M đến N là MAN, MBN, MABN có độ dài lần lượt bằng 14; 14; 17.
c) Ta có MANC là một đường đi từ M đến C.
M \({l_{MANC}}\; = {\rm{ }}{w_{MA}}\; + {\rm{ }}{w_{AN}}\; + {\rm{ }}{w_{NC}}\; = {\rm{ }}5{\rm{ }} + {\rm{ }}9{\rm{ }} + {\rm{ }}6{\rm{ }} = {\rm{ }}20,{\rm{ }}{l_{MBC}}\; = {\rm{ }}{w_{MB}}\; + {\rm{ }}{w_{BC}}\; = {\rm{ }}7{\rm{ }} + {\rm{ }}15{\rm{ }} = {\rm{ }}22.\)
Vì 20 < 22 nên \({l_{MANC}}\; < {\rm{ }}{l_{MBC}}.\)
Vậy MBC không phải là đường đi ngắn nhất từ M đến C.