Giải và trình bày phương pháp giải Giải bài 6.59 trang 26 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 6. Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình tương ứng…
Đề bài/câu hỏi:
Vẽ đồ thị mỗi hàm số sau, từ đó suy ra tập nghiệm của bất phương trình tương ứng
a) \(y = {x^2} – 3x + 2\) và bất phương trình \({x^2} – 3x + 2 \ge 0\)
b) \(y = {x^2} – x – 6\) và bất phương trình \({x^2} – x – 6 < 0\)
Lời giải:
a) \(y = {x^2} – 3x + 2\) và bất phương trình \({x^2} – 3x + 2 \ge 0\)
+) Vẽ đồ thị
Ta có: a = 1 > 0 nên parabol có bề lõm quay lên trên. Đỉnh \(I\left( {\frac{3}{2}; – \frac{1}{4}} \right)\). Trục đối xứng \(x = \frac{3}{2}\)
Giao điểm của đồ thị với trục Oy là (0 ; 2) và đồ thị cắt trục Ox tại 2 điểm có hoành độ là x = 1 và x = 2
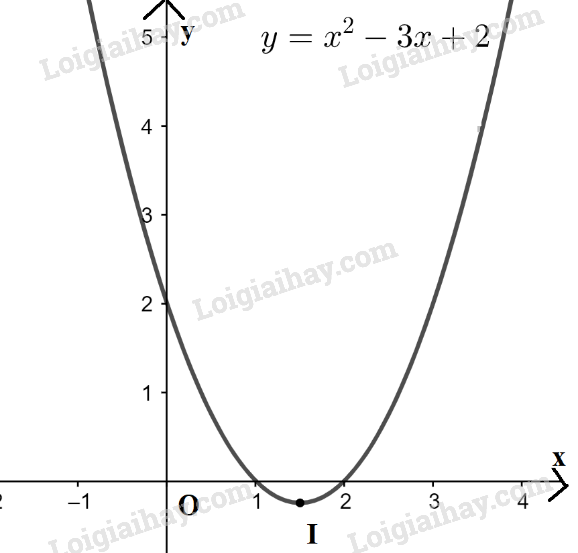
+) Giải BPT \({x^2} – 3x + 2 \ge 0\)
Từ đồ thị ta thấy với x ≤ 1 hoặc x ≥ 2 thì đồ thị hàm số \(y = {x^2} – 3x + 2\) nằm phía trên trục hoành.
Vậy tập nghiệm của BPT \({x^2} – 3x + 2 \ge 0\) là \(( – \infty ;1] \cup {\rm{[}}2; + \infty )\)
b) \(y = {x^2} – x – 6\) và bất phương trình \({x^2} – x – 6 < 0\)
+) Vẽ đồ thị
Ta có: a = 1 > 0 nên parabol có bề lõm quay lên trên. Đỉnh \(I\left( {\frac{1}{2}; – \frac{{25}}{4}} \right)\). Trục đối xứng \(x = \frac{1}{2}\)
Giao điểm của đồ thị với trục Oy là (0 ; -6) và đồ thị cắt trục Ox tại 2 điểm có hoành độ là x = 3 và x = -2
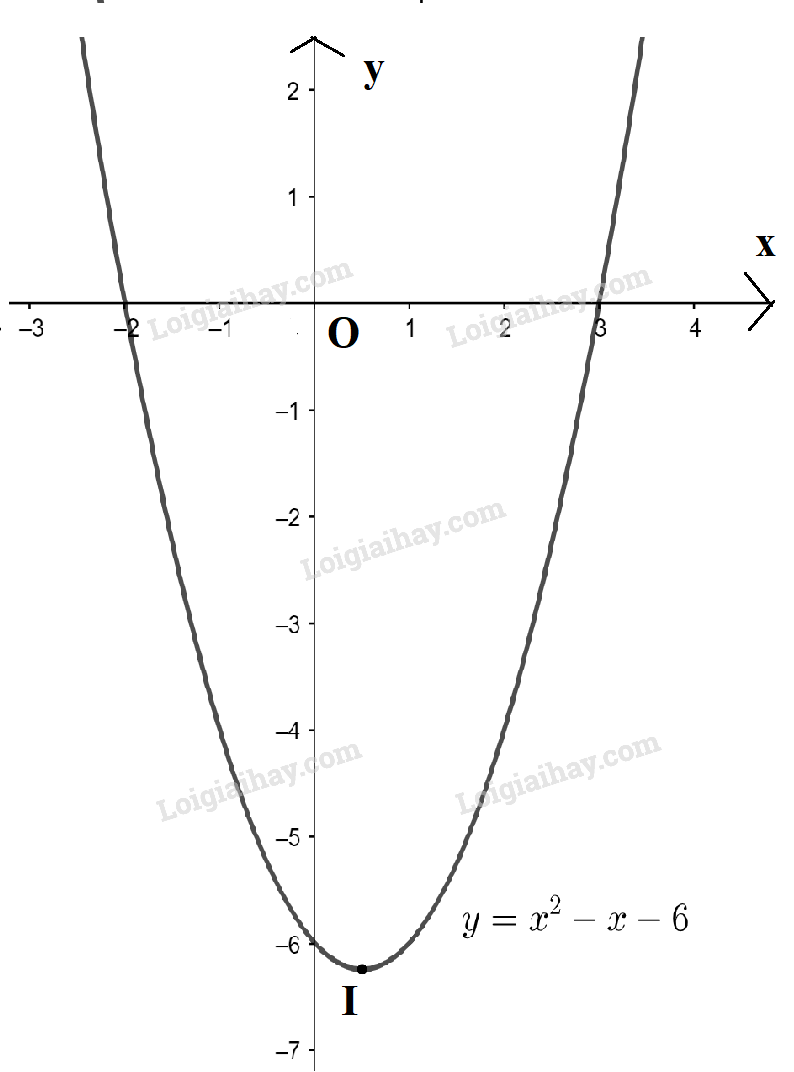
+) Giải BPT \({x^2} – x – 6 < 0\)
Từ đồ thị ta thấy với -2 < x < 3 thì đồ thị hàm số \(y = {x^2} – x – 6\) nằm phía dưới trục hoành.
Vậy tập nghiệm của BPT \({x^2} – x – 6 < 0\) là \(( – 2;3)\)