Phân tích và giải Giải bài 6.58 trang 26 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 6. Trong mỗi trường hợp dưới đây, hãy vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa…
Đề bài/câu hỏi:
Trong mỗi trường hợp dưới đây, hãy vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa độ rồi xác định tọa độ giao điểm của chúng
a) \(y = – x + 3\) và \(y = – {x^2} – 4x + 1\)
b) \(y = 2x – 5\) và \(y = {x^2} – 4x – 1\)
Lời giải:
a) \(y = – x + 3\) và \(y = – {x^2} – 4x + 1\)
+) Vẽ đồ thị
– Đồ thị hàm số \(y = – x + 3\) là đường thẳng đi qua 2 điểm (0;3) và (3;0)
– Đồ thị hàm số \(y = – {x^2} – 4x + 1\) là đường parabol có a = -1 < 0 nên có bề lõm quay xuống dưới.
Đỉnh \(I( – 2;5)\), trục đối xứng x = -2. Giao điểm của parabol với trục Oy là điểm (0 ; 1) và cắt trục Ox tại 2 điểm có hoành độ \(x = – 2 – \sqrt 5 \) và \(x = – 2 + \sqrt 5 \)
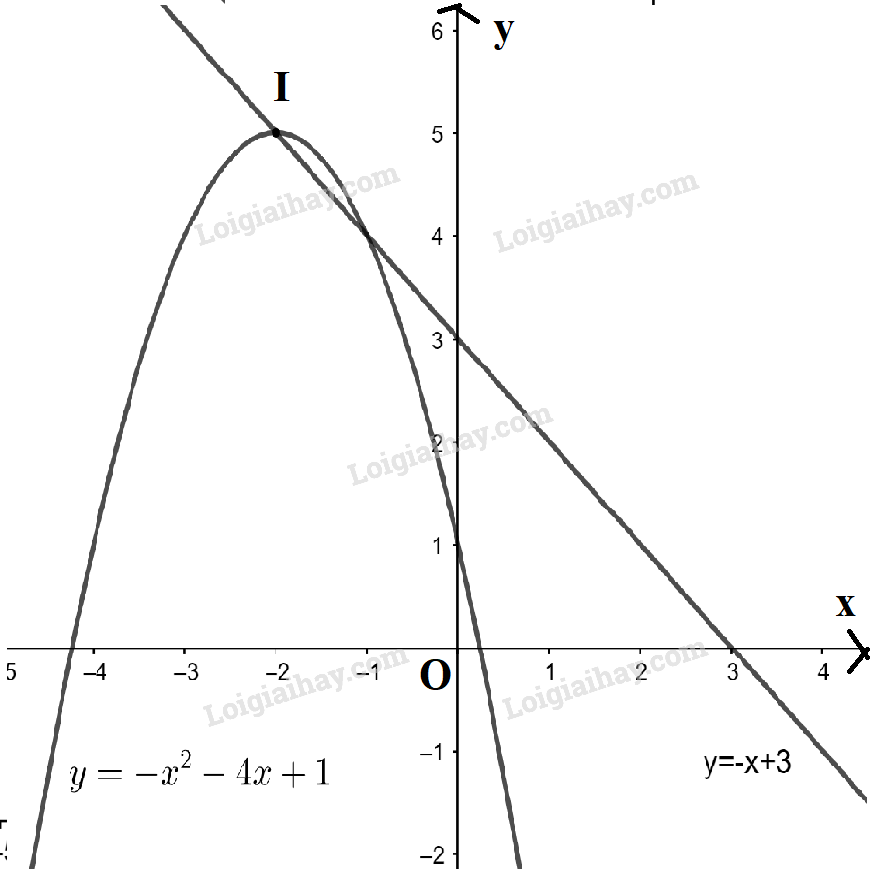
+) Tìm giao điểm
Xét phương trình hoành độ: \( – x + 3 = – {x^2} – 4x + 1 \Leftrightarrow – {x^2} – 3x – 2 = 0 \Leftrightarrow x = – 1\) hoặc x = -2
Với x = -1 thì y = 4 ; với x = -2 thì y = 5
Vậy giao điểm hai đồ thị là 2 điểm (-1 ; 4) và (-2 ; 5)
b) \(y = 2x – 5\) và \(y = {x^2} – 4x – 1\)
+) Vẽ đồ thị
– Đồ thị hàm số \(y = 2x – 5\) là đường thẳng đi qua 2 điểm (0 ; -5) và \(\left( {\frac{5}{2};0} \right)\)
– Đồ thị hàm số \(y = {x^2} – 4x – 1\) là đường parabol có a = 1 > 0 nên có bề lõm quay lên trên.
Đỉnh \(I(2; – 5)\), trục đối xứng x = 2. Giao điểm của parabol với trục Oy là điểm (0 ; -1) và cắt trục Ox tại 2 điểm có hoành độ \(x = 2 – \sqrt 5 \) và \(x = 2 + \sqrt 5 \)
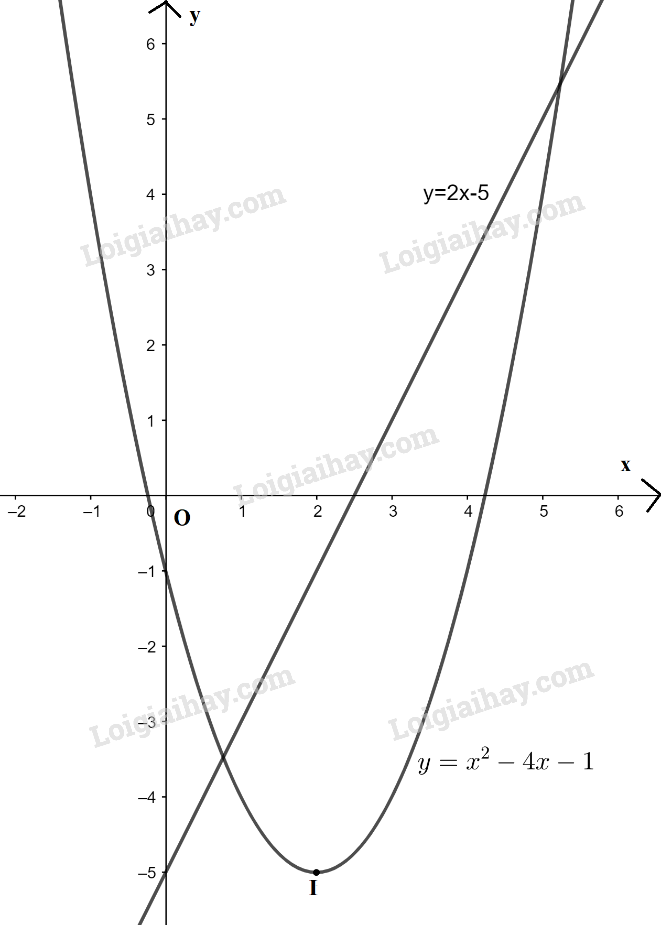
+) Tìm giao điểm
Xét phương trình hoành độ: \(2x – 5 = {x^2} – 4x – 1 \Leftrightarrow {x^2} – 6x + 4 = 0 \Leftrightarrow x = 3 – \sqrt 5 \) hoặc x = \(3 + \sqrt 5 \)
Với x = \(3 – \sqrt 5 \) thì y = \(1 – 2\sqrt 5 \) ; với x = \(3 + \sqrt 5 \) thì y = \(1 + 2\sqrt 5 \)
Vậy giao điểm hai đồ thị là 2 điểm (\(3 – \sqrt 5 \) ; \(1 – 2\sqrt 5 \)) và (\(3 + \sqrt 5 \) ; \(1 + 2\sqrt 5 \))