Phân tích, đưa ra lời giải Giải bài 6.55 trang 26 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 6. Tìm tập xác định của hàm số b) Vẽ đồ thị hàm số…
Đề bài/câu hỏi:
Cho hàm số : \(y = \left\{ \begin{array}{l}2x + 3, – 2 \le x < – 1\\\frac{1}{2}x + \frac{3}{2}, – 1 \le x < 1\\ – \frac{1}{2}x + \frac{9}{2},1 \le x \le 3\end{array} \right.\)
a) Tìm tập xác định của hàm số
b) Vẽ đồ thị hàm số
c) Từ đồ thị vẽ ở ý b) hãy chỉ ra các khoảng đồng biến, khoảng nghịch biến của hàm số
d) Tìm tập giá trị của hàm số
Lời giải:
a) Ta có: Hàm số xác định khi \({ – 2 \le x < – 1}\), \({ – 1 \le x < 1}\) và \({1 \le x \le 3}\) hay \(x \in [ – 2; – 1) \cup [ – 1;1) \cup [1;3]\)
=> tập xác định là \([ – 2; – 1) \cup [ – 1;1) \cup [1;3] = [-2 ; 3]\)
b) Đồ thị:
+ Vẽ đường thẳng \(y=2x+3\), giữ lại đường thẳng với \({ – 2 \le x < – 1}\) và bỏ phần còn lại.
+ Vẽ đường thẳng \(y=\frac{1}{2}x + \frac{3}{2}\), giữ lại đường thẳng với \({ – 2 \le x < – 1}\) và bỏ phần còn lại.
+ Vẽ đường thẳng \(y=-\frac{1}{2}x + \frac{9}{2}\), giữ lại đường thẳng với \({ 1 \le x \le 3}\) và bỏ phần còn lại.
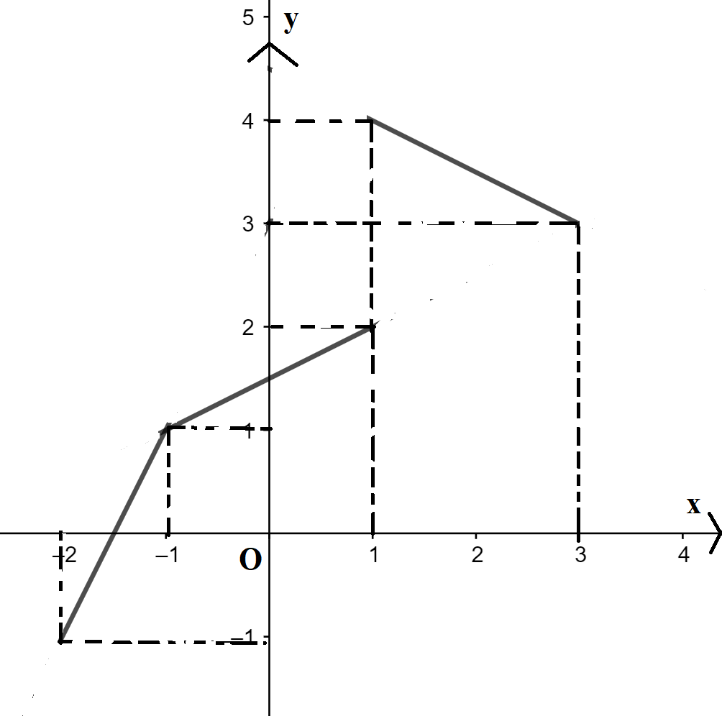
c) Quan sát từ trái sang phải:
+ Đồ thị hàm số đi lên trên khoảng (-2;-1) và (-1;2)
=> Hàm số đồng biến trên (-2 ; 1)
+ Đồ thị đi xuống trên (1;3) => Hàm số nghịch biến trên (1 ; 3)
d) Quang sát đồ thị,
+ với x thuộc [-2;1) thì giá trị của y thuộc [-1;2)
+ với x thuộc [1;3] thì giá trị của y thuộc [3;4]
=> Tập giá trị của hàm số là \([-1; 2) \cup {[3;4]}\)