Hướng dẫn giải Giải bài 4.65 trang 70 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài tập cuối Chương 4. Cho hình thang vuông ABCD…
Đề bài/câu hỏi:
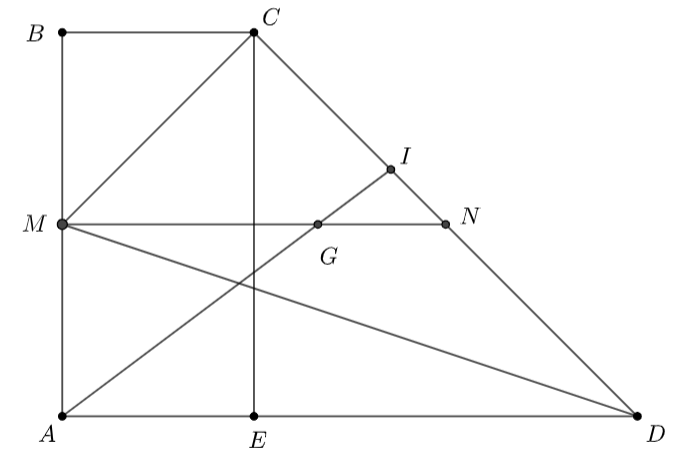
Cho hình thang vuông \(ABCD\) có \(\widehat {DAB} = \widehat {ABC} = {90^ \circ },\,\,BC = 1,\,\,AB = 2\) và \(AD = 3.\) Gọi \(M\) là trung điểm của \(AB.\)
a) Hãy biểu thị các vectơ \(\overrightarrow {CM} ,\,\,\overrightarrow {CD} \) theo hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} .\)
b) Gọi \(N\) là trung điểm của \(CD,\,\,G\) là trọng tâm tam giác \(MCD\) và \(I\) là điểm thuộc cạnh \(CD\) sao cho \(9IC = 5ID.\) Chứng minh rằng \(A,\,\,G,\,\,I\) thẳng hàng.
c) Tính độ dài các đoạn thẳng \(AI\) và \(BI.\)
Lời giải:
a) Ta có: \(BC = 1\) và \(AD = 3\)
mặt khác \(BC\)//\(AD\) vì \(ABCD\) là hình thang vuông tại \(A\) và \(B\)
\( \Rightarrow \) \(\overrightarrow {BC} = \frac{1}{3}\overrightarrow {AD} \)
Ta có: \(\overrightarrow {CM} = \overrightarrow {BM} – \overrightarrow {BC} = \frac{1}{2}\overrightarrow {AB} – \frac{1}{3}\overrightarrow {AD} \)
Ta có: \(\overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BA} + \overrightarrow {AD} \)
\(\begin{array}{l} = – \overrightarrow {BC} – \overrightarrow {AB} + \overrightarrow {AD} \\ = – \frac{1}{3}\overrightarrow {AD} – \overrightarrow {AB} + \overrightarrow {AD} \\ = \frac{2}{3}\overrightarrow {AD} – \overrightarrow {AB} \end{array}\)
b) Ta có: \(G\) là trọng tâm của \(\Delta MCD\)
\( \Rightarrow \) \(3\overrightarrow {AG} = \overrightarrow {AM} + \overrightarrow {AC} + \overrightarrow {AD} = \frac{1}{2}\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \overrightarrow {AD} = \frac{3}{2}\overrightarrow {AB} + \frac{4}{3}\overrightarrow {AD} \)
\( \Rightarrow \) \(6.3\overrightarrow {AG} = 18\overrightarrow {AG} = 9\overrightarrow {AB} + 8\overrightarrow {AD} \) (1)
Ta có: \(9IC = 5ID\)
\( \Rightarrow \) \(9\overrightarrow {IC} + 5\overrightarrow {ID} = \overrightarrow 0 \)
\( \Leftrightarrow \) \(9\left( {\overrightarrow {AC} – \overrightarrow {AI} } \right) + 5\left( {\overrightarrow {AD} – \overrightarrow {AI} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \) \(14\overrightarrow {AI} = 9\overrightarrow {AC} + 5\overrightarrow {AD} \)
\( \Leftrightarrow \) \(14\overrightarrow {AI} = 9\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + 5\overrightarrow {AD} = 9\overrightarrow {AB} + 9.\frac{1}{3}\overrightarrow {AD} + 5\overrightarrow {AD} \)
\( \Leftrightarrow \) \(14\overrightarrow {AI} = 9\overrightarrow {AB} + 8\overrightarrow {AD} \) (2)
Từ (1) và (2) \( \Rightarrow \) \(18\overrightarrow {AG} = 14\overrightarrow {AI} \)
\( \Rightarrow \) \(\overrightarrow {AG} \) và \(\overrightarrow {AI} \) cùng hướng
\( \Rightarrow \) ba điểm \(A,\,\,G,\,\,I\) thẳng hàng.
c) Ta có: \(14\overrightarrow {AI} = 9\overrightarrow {AB} + 8\overrightarrow {AD} \) (cmt)
\( \Rightarrow {\left( {14\overrightarrow {AI} } \right)^2} = {\left( {9\overrightarrow {AB} + 8\overrightarrow {AD} } \right)^2} = 81{\overrightarrow {AB} ^2} + 144\overrightarrow {AB} .\overrightarrow {AD} + 64{\overrightarrow {AD} ^2}\)
\( \Rightarrow 194A{I^2} = 81A{B^2} + 64A{D^2} = 81.4 + 64.9 = 900\)
\( \Rightarrow A{I^2} = \frac{{900}}{{196}}\)
\( \Rightarrow AI = \frac{{30}}{{14}} = \frac{{15}}{7}\)
Ta có: \(\overrightarrow {BI} = \overrightarrow {AI} – \overrightarrow {AB} = \frac{9}{{14}}\overrightarrow {AB} + \frac{4}{7}\overrightarrow {AD} – \overrightarrow {AB} = \frac{4}{7}\overrightarrow {AD} – \frac{5}{{14}}\overrightarrow {AB} \)
\( \Rightarrow \) \(B{I^2} = {\left( {\frac{4}{7}\overrightarrow {AD} – \frac{5}{{14}}\overrightarrow {AB} } \right)^2} = \frac{{16}}{{49}}{\overrightarrow {AD} ^2} – \frac{{20}}{{49}}\overrightarrow {AD} .\overrightarrow {AB} + \frac{{25}}{{196}}{\overrightarrow {AB} ^2}\)
\( \Rightarrow \) \(B{I^2} = \frac{{16}}{{49}}{\overrightarrow {AD} ^2} + \frac{{25}}{{196}}{\overrightarrow {AB} ^2} = \frac{{16}}{{49}}.9 + \frac{{25}}{{196}}.4 = \frac{{169}}{{49}}\)
\( \Rightarrow \) \(BI = \frac{{13}}{7}\)