Bài 4.33 trang 65 SBT toán 10 – Kết nối tri thức: Cho tam giác ABC không cân. Gọi D, E, F theo thứ tự là chân các đường cao kẻ từ A, B, C; gọi M, N, P tương ứng là trung điểm các cạnh BC, CA, AB.

Đề bài/câu hỏi:

Cho tam giác \(ABC\) không cân. Gọi \(D,\,\,E,\,\,F\) theo thứ tự là chân các đường cao kẻ từ \(A,\,\,B,\,\,C;\) gọi \(M,\,\,N,\,\,P\) tương ứng là trung điểm các cạnh \(BC,\,\,CA,\,\,AB.\) Chứng minh rằng \(\overrightarrow {MD} .\overrightarrow {BC} + \overrightarrow {NE} .\overrightarrow {CA} + \overrightarrow {PF} .\overrightarrow {AB} = 0\)

Hướng dẫn:

– Gọi \(H\) là trực tâm và \(O\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)

– Áp dụng định lý chiếu để tính tích vô hướng của các vectơ sau \(\overrightarrow {MD} .\overrightarrow {BC} ,\) \(\overrightarrow {NE} .\overrightarrow {CA} \) và \(\overrightarrow {PF} .\overrightarrow {AB} \)

Lời giải:

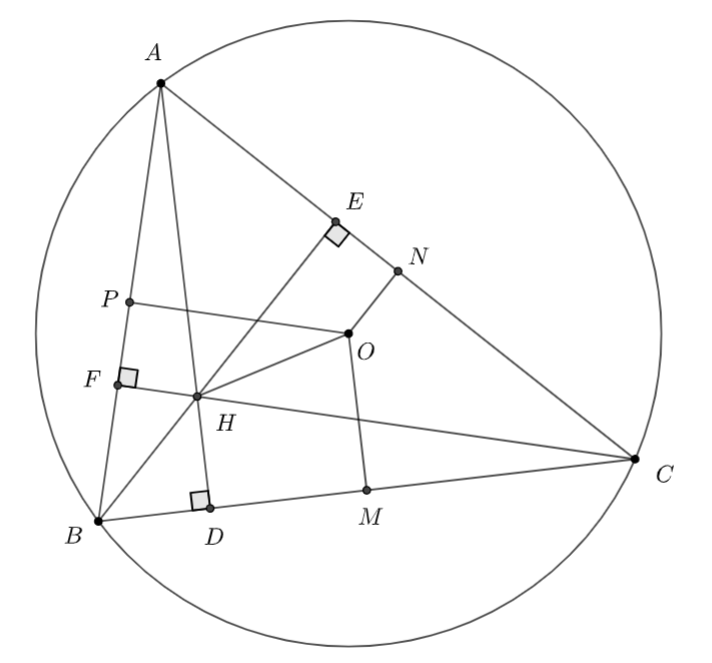
Gọi \(H\) là trực tâm và \(O\) là tâm đường tròn ngoại tiếp \(\Delta ABC\)

Ta có: \(ON \bot AC,\) \(OM \bot BC,\) \(OP \bot AB\) (quan hệ giữa đường kính và dây cung)

Áp dụng định lý chiếu ta có:

\(\overrightarrow {MD} .\overrightarrow {BC} = \overrightarrow {OH} .\left( {\overrightarrow {OC} – \overrightarrow {OB} } \right) = \overrightarrow {OH} .\overrightarrow {OC} – \overrightarrow {OH} .\overrightarrow {OB} \) (1)

\(\overrightarrow {NE} .\overrightarrow {CA} = \overrightarrow {OH} .\left( {\overrightarrow {OA} – \overrightarrow {OC} } \right) = \overrightarrow {OH} .\overrightarrow {OA} – \overrightarrow {OH} .\overrightarrow {OC} \) (2)

\(\overrightarrow {PF} .\overrightarrow {AB} = \overrightarrow {OH} .\left( {\overrightarrow {OB} – \overrightarrow {OA} } \right) = \overrightarrow {OH} .\overrightarrow {OB} – \overrightarrow {OH} .\overrightarrow {OA} \) (3)

Từ (1), (2) và (3) \( \Rightarrow \) \(\overrightarrow {MD} .\overrightarrow {BC} + \overrightarrow {NE} .\overrightarrow {CA} + \overrightarrow {PF} .\overrightarrow {AB} = 0\) (đpcm)