Tính các vectơ \(\overrightarrow {AM} \) và \(\overrightarrow {DE} \) xong chứng minh tích vô hướng \(\overrightarrow {AM} . \overrightarrow {DE} = 0\. Gợi ý giải Giải bài 4.31 trang 65 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 11. Tích vô hướng của hai vectơ. AM vuông góc với DE. b) BE vuông góc với CD….
Đề bài/câu hỏi:
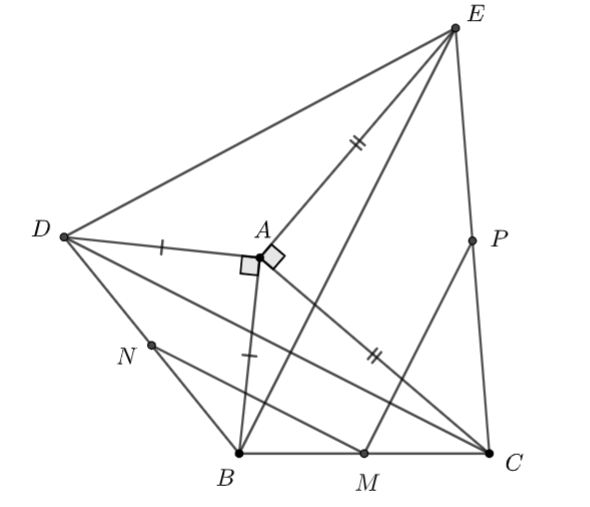
Cho tam giác \(ABC\) có \(\widehat A < {90^ \circ }.\) Dựng ra phía ngoài tam giác hai tam giác vuông cân đỉnh \(A\) là \(ABD\) và \(ACE.\) Gọi \(M,\,\,N,\,\,P\) theo thứ tự là trung điểm \(BC,\,\,BD,\,\,CE.\) Chứng minh rằng:
a) \(AM\) vuông góc với \(DE.\)
b) \(BE\) vuông góc với \(CD.\)
c) Tam giác \(MNP\) là một tam giác vuông cân.
Hướng dẫn:
– Tính các vectơ \(\overrightarrow {AM} \) và \(\overrightarrow {DE} \) xong chứng minh tích vô hướng \(\overrightarrow {AM} .\overrightarrow {DE} = 0\)
– Tính các vectơ \(\overrightarrow {BE} \) và \(\overrightarrow {CD} \) xong chứng minh tích vô hướng \(\overrightarrow {BE} .\overrightarrow {CD} = 0\)
– Chứng minh \(MN\)//\(CD\) và \(MP\)//\(BE\)
Lời giải:
a) Ta có: \(\overrightarrow {DE} = \overrightarrow {AE} – \overrightarrow {AD} \) và \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
\( \Rightarrow \overrightarrow {AM} .\overrightarrow {DE} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\left( {\overrightarrow {AE} – \overrightarrow {AD} } \right)\)
\(\begin{array}{l} = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AE} – \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AC} .\overrightarrow {AE} – \overrightarrow {AC} .\overrightarrow {AD} } \right)\\ = \frac{1}{2}\left( {\overrightarrow {AB} .\overrightarrow {AE} – \overrightarrow {AC} .\overrightarrow {AD} } \right)\\ = \frac{1}{2}\left( {AB.AE.\cos \widehat {BAE} – AC.AD.\cos \widehat {CAD}} \right) = 0\end{array}\)
\( \Rightarrow \) \(\overrightarrow {AM} \bot \overrightarrow {DE} \) \( \Rightarrow \) \(AM \bot DE\)
b) Ta có: \(\overrightarrow {BE} = \overrightarrow {AE} – \overrightarrow {AB} \) và \(\overrightarrow {CD} = \overrightarrow {AD} – \overrightarrow {AC} \)
\( \Rightarrow \) \(\overrightarrow {BE} .\overrightarrow {CD} = \left( {\overrightarrow {AE} – \overrightarrow {AB} } \right)\left( {\overrightarrow {AD} – \overrightarrow {AC} } \right)\)
\(\begin{array}{l} = \overrightarrow {AE} .\overrightarrow {AD} – \overrightarrow {AE} .\overrightarrow {AC} – \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} \\ = \overrightarrow {AE} .\overrightarrow {AD} + \overrightarrow {AB} .\overrightarrow {AC} \\ = AE.AD.\cos \widehat {DAE} + AB.AC.\cos \widehat {BAC}\\ = AE.AD.\cos \widehat {DAE} + AB.AC.\cos \left( {{{180}^ \circ } – \widehat {DAE}} \right) = 0\end{array}\)
\( \Rightarrow \) \(\overrightarrow {BE} \bot \overrightarrow {CD} \) \( \Rightarrow \) \(BE \bot CD\)
c) Ta có: \(MN\) và \(MP\) lần lượt là đường trung bình của \(\Delta BCD\) và \(\Delta ACE\)
\( \Rightarrow \) \(MN\)//\(CD\) và \(MP\)//\(BE\)
mặt khác \(CD \bot BE\) (cm câu b)
\( \Rightarrow \) \(MN \bot MP\)
\( \Rightarrow \) \(\Delta MNP\) vuông tại \(M\)
+
Xét \(\Delta ADC\) và \(\Delta ABE\) ta có:
\(AD = AB\)
\(AC = AE\)
\(\widehat {DAC} = \widehat {BAE} = {90^o} + \widehat {BAC}\)
\( \Rightarrow \Delta ADC = \Delta ABE\) (cạnh góc cạnh)
\( \Rightarrow DC = BE\)
Lại có: \(MN = \frac{1}{2}DC\) (do M, N là trung điểm BD, BC)
\(MP = \frac{1}{2}BE\) (do M, N là trung điểm CB, CE)
\( \Rightarrow MN = MP\)
Vậy tam giác MNP vuông cân tại M.