Trả lời Giải bài 4.22 trang 58 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 10. Vectơ trong mặt phẳng tọa độ. Trong mặt phẳng tọa độ Oxy cho ba điểm M(4;0),N(5;2) và P(2;3)….
Đề bài/câu hỏi:
Trong mặt phẳng tọa độ \(Oxy\) cho ba điểm \(M(4;0),\,\,N(5;2)\) và \(P(2;3).\) Tìm tọa độ các đỉnh của tam giác \(ABC,\) biết \(M,\,\,N,\,\,P\) theo thứ tự là trung điểm các cạnh \(BC,\,\,CA,\,\,AB.\)
Lời giải:
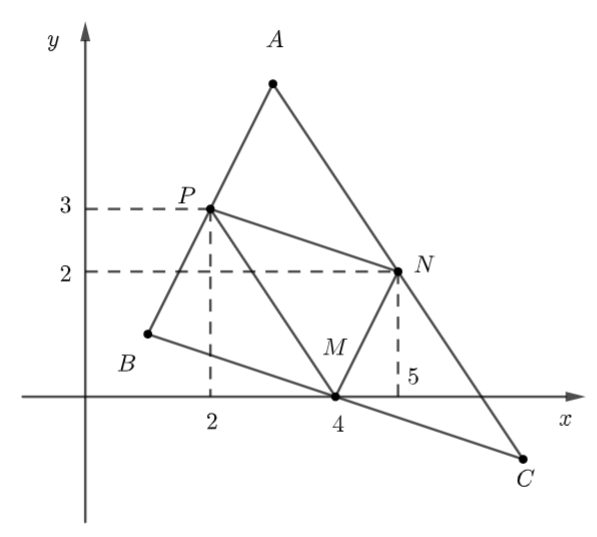
Ta có: \(MN,\,\,NP,\,\,MP\) là đường trung bình của \(\Delta ABC\)
\( \Rightarrow \) \(MN\)//\(AB\), \(NP\)//\(BC\), \(MP\)//\(AC\).
\( \Rightarrow \) \(APMN\), \(BPNM\), \(CMPN\) là hình bình hành
Xét hình bình hành \(APMN\) có:
\(\begin{array}{l}\overrightarrow {OA} = \overrightarrow {OP} + \overrightarrow {ON} – \overrightarrow {OM} \\ \Rightarrow \overrightarrow {OA} = (2;3) + (5;2) – (4;0) = (3;5)\end{array}\)
\( \Rightarrow \) Tọa độ điểm \(A\) là: \(A(3;5).\)
Xét hình bình hành \(BPNM\) có:
\(\begin{array}{l}\overrightarrow {OB} = \overrightarrow {OP} + \overrightarrow {OM} – \overrightarrow {ON} \\ \Rightarrow \overrightarrow {OB} = (2;3) + (4;0) – (5;2) = (1;1)\end{array}\)
\( \Rightarrow \) Tọa độ điểm \(B\) là: \(B(1;1).\)
Xét hình bình hành \(CMPN\) có:
\(\begin{array}{l}\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {OM} – \overrightarrow {OP} \\ \Rightarrow \overrightarrow {OC} = (5;2) + (4;0) – (2;3) = (7; – 1)\end{array}\)
\( \Rightarrow \) Tọa độ điểm \(C\) là: \(C(7; – 1).\)