Đổi 30 phút = \(\frac{1}{2}\) giờ và 36 phút = \(\frac{3}{5}\) giờ Tính \(\widehat {ABC}\) Tính quãng đường \(AB, \, \, BC\. Hướng dẫn giải Giải bài 3.11 trang 39 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 6. Hệ thức lượng trong tam giác. Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng),…
Đề bài/câu hỏi:
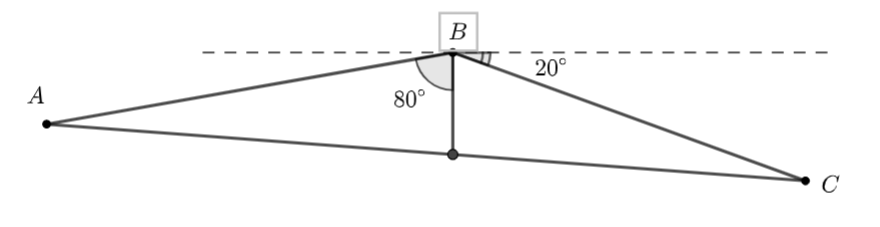
Một tàu du lịch xuất phát từ bãi biển Đồ Sơn (Hải Phòng), chạy theo hướng \(N{80^ \circ }E\) với vận tốc 20 km/h. Sau khi đi được 30 phút, tàu chuyển sang hướng\(E{20^ \circ }S\) giữ nguyên vận tốc và chạy tiếp 36 phút nữa đến đảo Cát Bà. Hỏi khi đó tàu du lịch cách vị trí xuất phát bao nhiêu ki lô mét.
Hướng dẫn:
– Đổi 30 phút = \(\frac{1}{2}\) giờ và 36 phút = \(\frac{3}{5}\) giờ
– Tính \(\widehat {ABC}\)
– Tính quãng đường \(AB,\,\,BC\)
– Áp dụng định lý côsin để tính quãng đường \(A{C^2} = A{B^2} + B{C^2} – 2AB.BC.\cos ABC\)
Lời giải:
Xét \(\Delta ABC\) có \(\widehat B = {80^ \circ } + \left( {{{90}^ \circ } – {{20}^ \circ }} \right) = {150^ \circ }.\)
Độ dài quãng đường \(AB\) là: \(AB = 20.\frac{1}{2} = 10\,\,km.\)
Độ dài quãng đường \(BC\) là: \(BC = 20.\frac{3}{5} = 12\,\,km.\)
Khoảng cách từ điểm xuất phát A đến điểm đích C là:
Áp dụng định lý côsin, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} – 2AB.BC.\cos ABC\\A{C^2} = {10^2} + {12^2} – 2.10.12.\cos {150^ \circ }\\A{C^2} = 100 + 144 – 240.\left( {\frac{{ – \sqrt 3 }}{2}} \right) \approx 452.\\ \Rightarrow \,\,AC \approx \sqrt {452} \approx 21\,\,km.\end{array}\)