Vẽ các hệ bất phương trình trên mặt phẳng tọa độ \(Oxy. \. Phân tích và giải Giải bài 2.6 trang 23 sách bài tập toán 10 – Kết nối tri thức với cuộc sống – Bài 4. Hệ bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm của các hệ bất phương trình sau trên mặt phẳng tọa độ:…
Đề bài/câu hỏi:
Biểu diễn miền nghiệm của các hệ bất phương trình sau trên mặt phẳng tọa độ:
a) \(\left\{ {\begin{array}{*{20}{c}}{x \ge – 1}\\{y \ge 0}\\{x + y \le 4}\end{array}} \right.\)
b) \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{y > 0}\\{x – y – 4 < 0}\end{array}} \right.\)
c) \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{x \le 3}\\{x \ge – 1}\\{y \ge – 2}\end{array}} \right.\)
Hướng dẫn:
– Vẽ các hệ bất phương trình trên mặt phẳng tọa độ \(Oxy.\)
– Nhìn vào đồ thị xác định miền nghiệm của hệ bất phương trình đã cho.
Lời giải:
a) \(\left\{ {\begin{array}{*{20}{c}}{x \ge – 1}\\{y \ge 0}\\{x + y \le 4}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(x \ge – 1\) là nửa mặt phẳng bờ \(d:x = – 1\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(y \ge 0\) là nửa mặt phẳng bờ \(Ox\) chứa điểm \(\left( {0;4} \right).\)
Xác định miền nghiệm của bất phương trình\(x + y \le 4.\)
Vẽ đường thẳng \({d_2}:x + y = 4\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(x + y,\) ta được \(0 + 0 = 0 < 4.\)
Do đó, miền nghiệm của bất phương trình \({d_2}:x + y = 4\) là nửa mặt phẳng bờ \({d_2}\) và chứa điểm \(O\left( {0;0} \right).\)
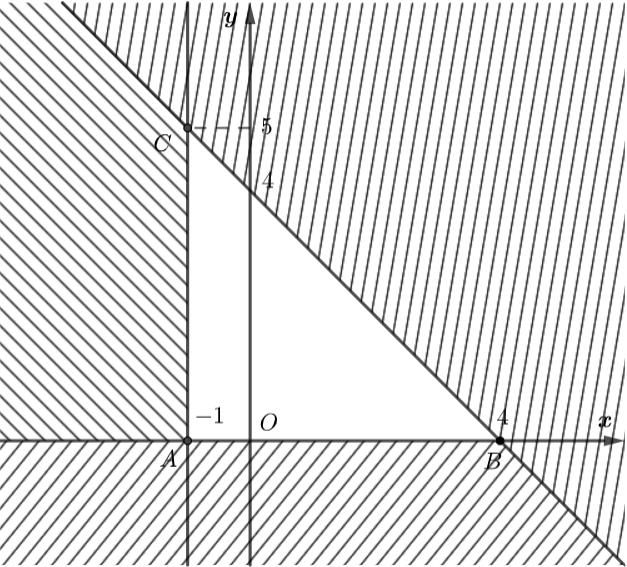
Vậy miền nghiệm của hệ bất phương trình trên là: \(\Delta ABC\) với \(A\left( { – 1;0} \right),\,\,B\left( {4;0} \right),\,\,C\left( { – 1;5} \right).\)
b) \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{y > 0}\\{x – y – 4 < 0}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(x > 0\) là nửa mặt phẳng bờ \(Oy\) chứa điểm \(\left( {1;0} \right)\) mà bỏ đi trục \(Oy.\)
Xác định miền nghiệm của bất phương trình \(y > 0\) là nửa mặt phẳng bờ \(Ox\) chứa điểm \(\left( {0;1} \right)\) mà bỏ đi trục \(Ox.\)
Xác định miền nghiệm của bất phương trình \(x – y – 4 < 0\).
Vẽ đường thẳng \({d_2}:x – y – 4 = 0\) trên mặt phẳng tọa độ \(Oxy.\)
Chọn \(O\left( {0;0} \right)\) không thuộc đường thẳng \({d_2}\) và thay vào biểu thức \(x – y – 4,\) ta được \(0 – 0 – 4 = – 4 < 0.\)
Do đó, miền nghiệm của bất phương trình \(x – y – 4 < 0\) là nửa mặt phẳng bờ \({d_2}\) chứa điểm \(O\left( {0;0} \right)\) không kể \({d_2}\).
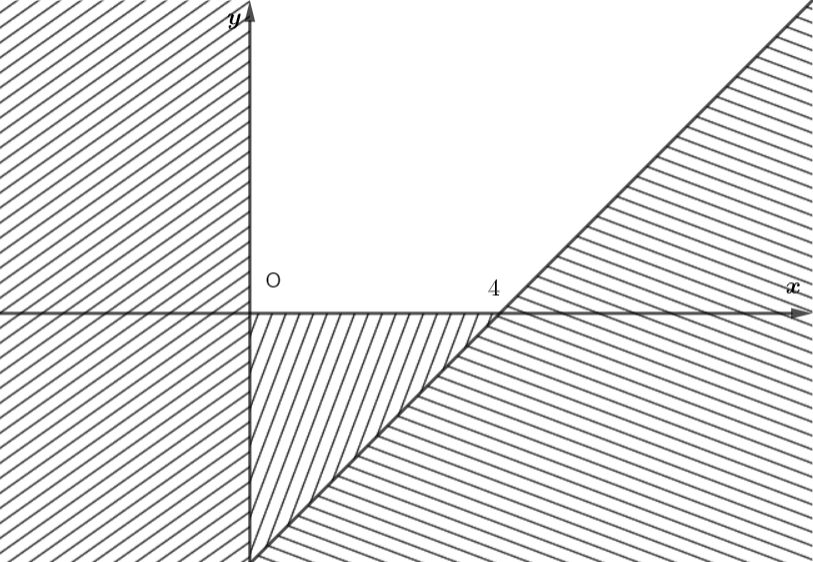
Miền nghiệm của hệ bất phương trình trên là phần không có gạch.
c) \(\left\{ {\begin{array}{*{20}{c}}{y \le 3}\\{x \le 3}\\{x \ge – 1}\\{y \ge – 2}\end{array}} \right.\)
Xác định miền nghiệm của bất phương trình \(y \le 3\) là nửa mặt phẳng bờ \(d:y = 3\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(x \le 3\) là nửa mặt phẳng bờ \({d_1}:x = 3\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(x \ge – 1\) là nửa mặt phẳng bờ \({d_3}:x = – 1\) chứa điểm \(O\left( {0;0} \right).\)
Xác định miền nghiệm của bất phương trình \(y \ge – 2\) là nửa mặt phẳng bờ \({d_4}:y = – 2\) chứa điểm \(O\left( {0;0} \right).\)
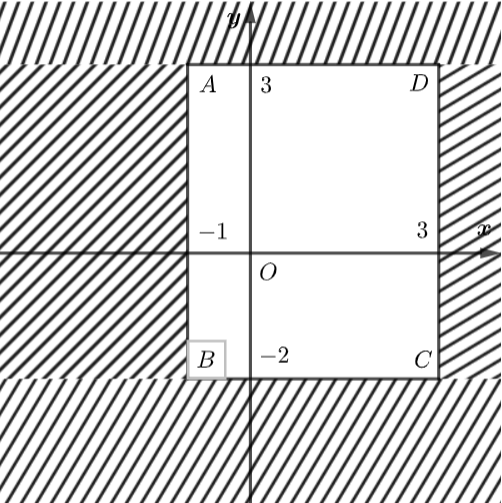
Miền nghiệm của hệ bất phương trình trên là: hình chữ nhật \(ABCD\) với \(A\left( { – 1;3} \right),\,\,B\left( { – 1; – 2} \right),\,\,C\left( {3; – 2} \right),\,\,D\left( {3;3} \right).\)