Trả lời Luyện tập 3 Bài 6. Hệ thức lượng trong tam giác (trang 40, 41) – SGK Toán 10 Kết nối tri thức. Tham khảo: Tính độ dài các cạnh và các góc còn lại của tam giác.
Câu hỏi/Đề bài:
Giải tam giác ABC, biết b = 32, c =45, \(\widehat A = {87^o}\)
Hướng dẫn:
Tính độ dài các cạnh và các góc còn lại của tam giác.
Bước 1: Tính a: \({a^2} = {b^2} + {c^2} – 2.bc.\cos A\)
Bước 2: Tính sinB, suy ra góc B, góc C.
Lời giải:
Ta cần tính cạnh BC, góc B và góc C.
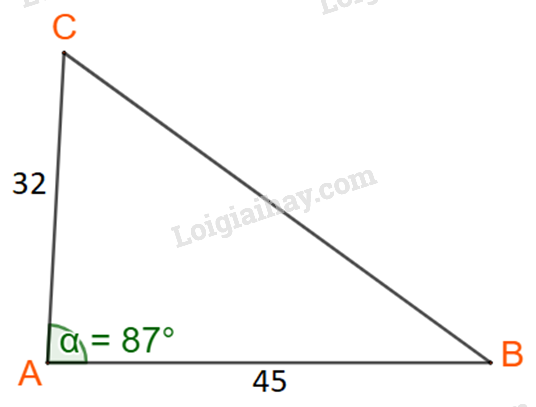
Áp dụng định lí cosin tại đỉnh A ta có:
\({a^2} = {b^2} + {c^2} – \,2b\,c.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {32^2} + {45^2} – 2.32.45.\cos {87^o}\\ \Leftrightarrow B{C^2} \approx 2898,27\\ \Leftrightarrow BC \approx 53,8\end{array}\)
Theo định lí sin, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \Rightarrow \sin B = \frac{{b.\sin A}}{a} = \frac{{32.\sin {{87}^o}}}{{53,8}} \approx 0,594.\)
\( \Rightarrow \widehat B \approx 36,{44^o}\) hoặc \(\widehat B \approx 143,{56^o}\)(Loại vì \(\widehat A + \widehat B = 230,{56^o} > {180^o}\))
\( \Rightarrow \widehat C = {180^o} – \widehat A – \widehat B \approx {180^o} – {87^o} – 36,{44^o} = 56,{56^o}\)
Vậy tam giác ABC có \(BC \approx 53,8\); \(\widehat B \approx 36,{44^o}\) và \(\widehat C = 56,{56^o}\).