Đáp án Hoạt động 5 Bài 6. Hệ thức lượng trong tam giác (trang 41, 42) – SGK Toán 10 Kết nối tri thức. Tham khảo: Biểu thị BD dựa vào sin A (hoặc \(\sin \left( {{{180}^o} – {\rm{ }}A} \right)\.
Câu hỏi/Đề bài:
Cho tam giác ABC với đường cao BD.
a) Biểu thị BD theo AB và sinA.
b) Viết công thức tính diện tích S của tam giác ABC theo b,c, sin A.
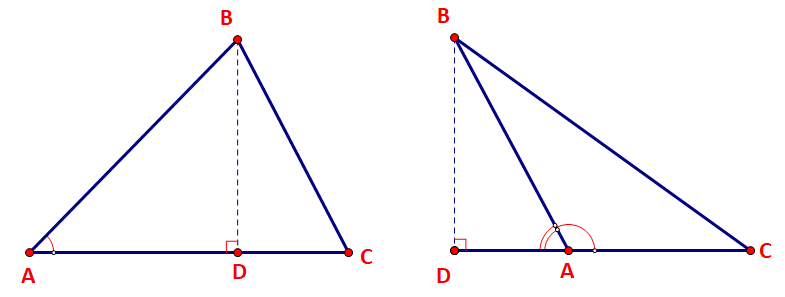
Hướng dẫn:
a) Biểu thị BD dựa vào sin A (hoặc \(\sin \left( {{{180}^o} – {\rm{ }}A} \right)\)) trong tam giác vuông ABD.
b)
+) Tính \({S_{ABC}} = \frac{1}{2}BD.AC\)
+) Thay BD ở ý a) để suy ra công thức tính S theo b,c và sin A.
Lời giải:
a) Xét tam giác vuông ABD vuông tại D ta có:
TH1: góc A nhọn
\(\sin A = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
TH2: góc A tù
\(\sin A = \sin ({180^o} – A) = \frac{{BD}}{{AB}} \Rightarrow BD = AB.\sin A\)
Vậy \(BD = AB.\sin A\)
b) Ta có diện tích S của tam giác ABC là: \(S = \frac{1}{2}BD.AC\)
Mà \(BD = AB.\sin A = c.\sin A\); BC = a. Thế vào (*) ta được:
\(S = \frac{1}{2}c.\sin A.b\) hay \(S = \frac{1}{2}bc.\sin A.\)
Vậy diện tích S của tam giác ABC theo b, c, sin A là \(S = \frac{1}{2}bc.\sin A.\)