Trả lời Hoạt động 4 Bài 6. Hệ thức lượng trong tam giác (trang 41, 42) – SGK Toán 10 Kết nối tri thức. Gợi ý: Tính diện tích tam giác ABC theo diện tích các tam giác IBC, ICA, IAB.
Câu hỏi/Đề bài:
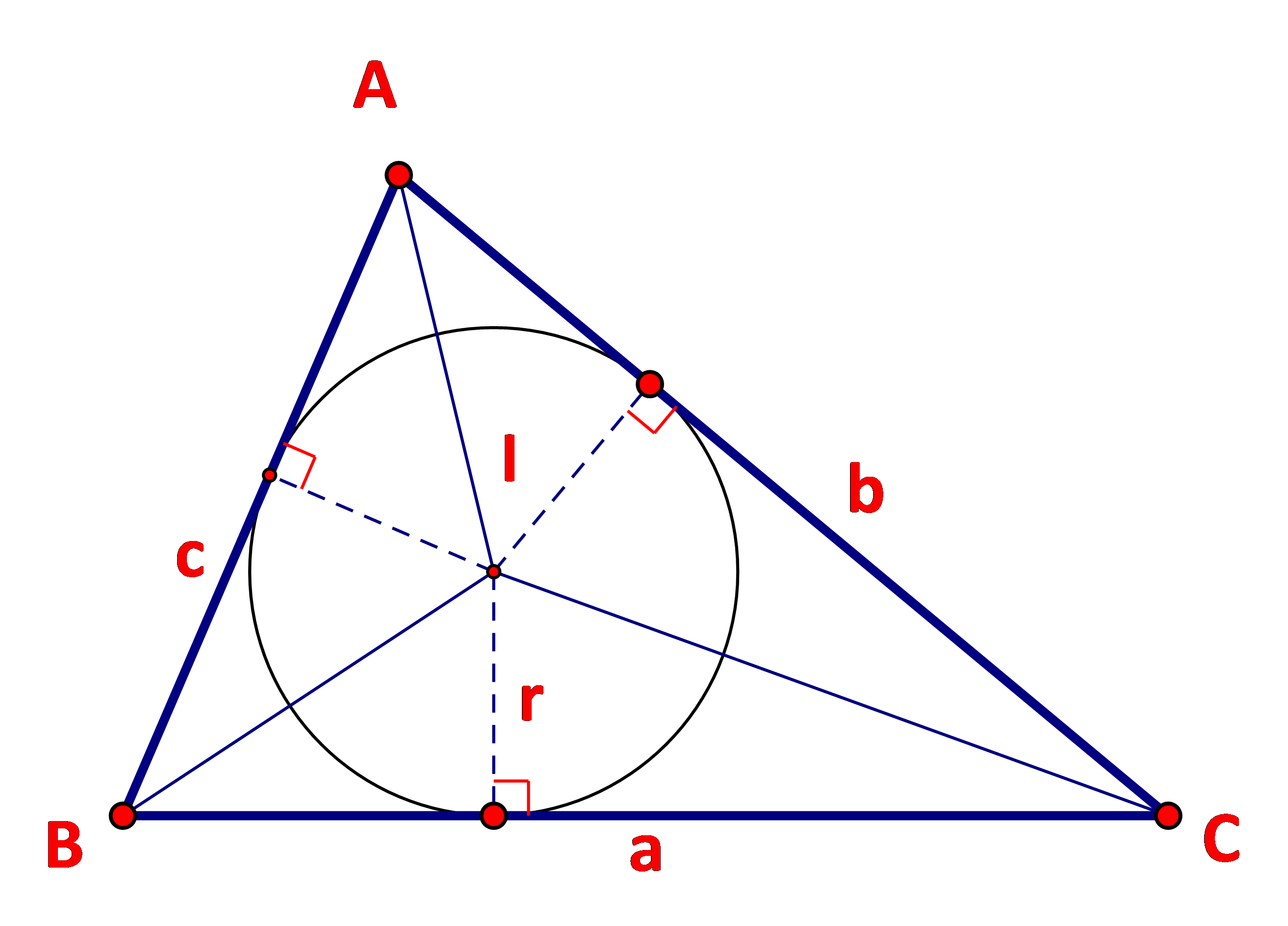
Cho tam giác ABC với I là tâm đường trong nội tiếp tam giác.
a) Nêu mối liên hệ giữa diện tích tam giác ABC và diện tích các tam giác IBC, ICA, IAB.
b) Tính diện tích tam giác ABC theo r,a,b,c.
Hướng dẫn:
a) Tính diện tích tam giác ABC theo diện tích các tam giác IBC, ICA, IAB.
b) Diện tích tam giác IBC: \({S_{IBC}} = \frac{1}{2}r.a\).
Lời giải:
a) Diện tích tam giác ABC là: \[S = {S_{IAB}} + {S_{IBC}} + {S_{IAC}}\]
b)
Kí hiệu: D,E, F lần lượt là hình chiếu của I trên AB, BC, AC.
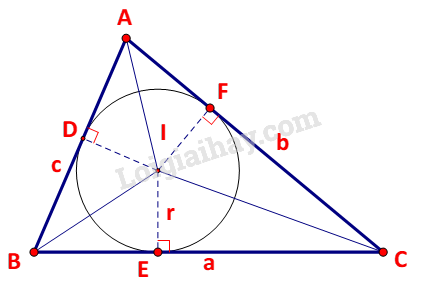
Ta có:
\(\begin{array}{l}{S_{IAB}} = \frac{1}{2}.ID.AB = \frac{1}{2}r.c\\{S_{IBC}} = \frac{1}{2}IE.BC = \frac{1}{2}r.a\\{S_{IAC}} = \frac{1}{2}IF.AC = \frac{1}{2}r.b\end{array}\)
\( \Rightarrow S = \frac{1}{2}r.c + \frac{1}{2}r.a + \frac{1}{2}r.b = \frac{1}{2}r.\left( {a + b + c} \right)\)
Vậy diện tích tam giác ABC tính theo r, a, b, c là \(S = \frac{1}{2}r.\left( {a + b + c} \right)\).