Đáp án Hoạt động 2 Bài 4. Hệ bất phương trình bậc nhất hai ẩn (trang 28, 29) – SGK Toán 10 Kết nối tri thức. Gợi ý: Biểu diễn các miền nghiệm của từng bất phương trình \(x \ge 0;y \ge 0\.
Câu hỏi/Đề bài:
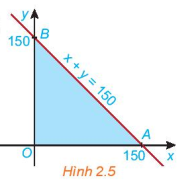
Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
a) Xác định miền nghiệm \({D_1},{D_2},{D_3}\) của các bất phương trình tương ứng \(x \ge 0;y \ge 0\) và \(x + y \le 150\).
b) Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\) hay không?
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Hướng dẫn:
a) Biểu diễn các miền nghiệm của từng bất phương trình \(x \ge 0;y \ge 0\) và \(x + y \le 150\)
Bước 1: Vẽ đường thẳng (nét liền) \(ax + by = c\).
Bước 2: Lấy điểm một điểm không thuộc đường thẳng \(ax + by = c\) và thay vào bất phương trình cần xác định miền nghiệm.
Bước 3: Nếu tọa độ điểm đó thỏa mãn bất phương trình thì miền nghiệm của bất phương trình chứa điểm đó.
b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.
Lời giải:
a)
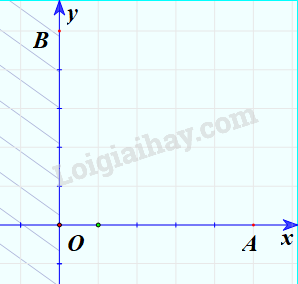
Miền nghiệm của bất phương trình \(x \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(x = 0\). Đây là trục Oy.
Bước 2: Lấy điểm A(150;0) không thuộc trục Oy và thay vào biểu thức \(x\), ta được: \(x = 150 \ge 0\).
Bước 3: Do điểm A thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm A.
Minh họa (phần không bị gạch chéo):
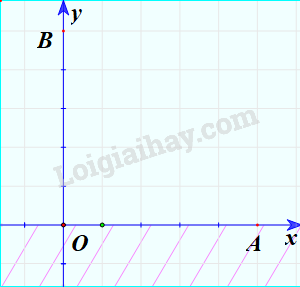
Miền nghiệm của bất phương trình \(y \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(y = 0\). Đây là trục Ox.
Bước 2: Lấy điểm B(0;150) không thuộc trục Ox và thay vào biểu thức \(y\), ta được: \(y = 150 \ge 0\).
Bước 3: Do điểm B thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm B.
Minh họa (phần không bị gạch chéo):
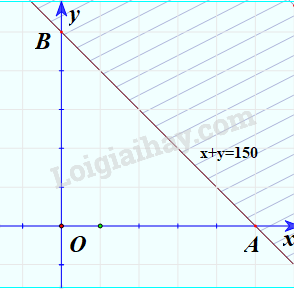
Miền nghiệm của bất phương trình \(x + y \le 150\):
Bước 1: Vẽ đường thẳng (nét liền) \(x + y = 150\).
Bước 2: Lấy điểm O(0;0) không thuộc đường thẳng \(x + y = 150\) và thay vào \(x + y\), ta được: \(0 + 0 = 0 \le 150\)
Bước 3: Do điểm O thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm O.
Minh họa (phần không bị gạch chéo):
Vậy \({D_1}\) là nửa trên mặt phẳng có bờ là trục Oy, \({D_2}\) là nửa bên phải mặt phẳng có bờ là trục Ox và \({D_3}\) là nửa mặt phẳng có bờ là đường thẳng x+y=150 chứa điểm O.
b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.
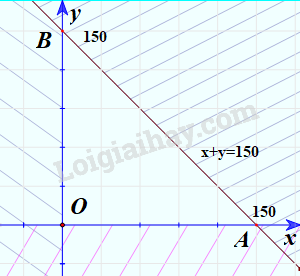
=>Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\)
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;2) trong tam giác OAB, thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{2 \ge 0}\\{1 + 2 \le 150}\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;2) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;149), thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{149 \ge 0}\\{1 + 149 \le 150}\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;149) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)