Bước 1: Tính AC: \(A{C^2} = B{C^2} + B{A^2} – 2. BC. BA. \cos ABC\) Bước 2: Tính góc ACB, suy ra góc ACD. Hướng dẫn giải Giải bài 3.11 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức – Bài 6. Hệ thức lượng trong tam giác. Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19….
Đề bài/câu hỏi:
Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
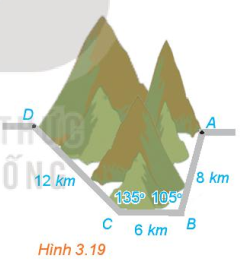
Hướng dẫn:
Bước 1: Tính AC: \(A{C^2} = B{C^2} + B{A^2} – 2.BC.BA.\cos ABC\)
Bước 2: Tính góc ACB, suy ra góc ACD.
Bước 3: Tính AD: \(A{D^2} = D{C^2} + C{A^2} – 2.DC.CA\cos ACD\)
Bước 4: Tính số kilomet giảm đi so với đường cũ.
Lời giải:
Bước 1:
Áp dụng định lí cos trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = {6^2} + {8^2} – 2.6.8.\cos {105^o}\\ \Rightarrow AC \approx 11,1735\;(km)\end{array}\)
Bước 2:
Lại có: Theo định lí sin thì
\(\begin{array}{l}\frac{{AB}}{{\sin ACB}} = \frac{{AC}}{{\sin ABC}} \Rightarrow \sin ACB = \frac{{8.\sin {{105}^o}}}{{11,1735}}\\ \Rightarrow \widehat {ACB} \approx 44^o\\ \Rightarrow \widehat {ACD} = {135^o} – 44^o = 91^o\end{array}\)
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
\(\begin{array}{l}A{D^2} = {12^2} + 11,{1735^2} – 2.12.11,1735\cos 91^o\\ \Rightarrow AD \approx 16,5387\;(km)\end{array}\)
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là: \(12 + 6 + 8 – 16,5387 = 9,4613\;(km)\)