Đáp án Thực hành 2 Bài 2. Tổng và hiệu của hai vectơ (trang 88, 89, 90) – SGK Toán 10 Chân trời sáng tạo. Tham khảo: Bước 1: Dựng hình bình hành ABDC.
Câu hỏi/Đề bài:
Cho tam giác đều ABC cạnh có độ dài là a. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC}\)
Hướng dẫn:
Bước 1: Dựng hình bình hành ABDC
Bước 2: Áp dụng quy tắc hình bình hành tìm tổng vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \)
Bước 3: Tìm độ dài vectơ tổng.
Lời giải:
Dựng hình bình hành ABDC.
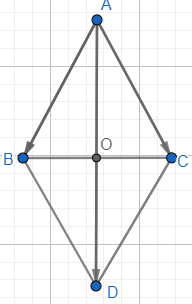
Áp dụng quy tắc hình bình hành vào ABDC ta có:
\(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD\)
Gọi O là giao điểm của AD và BC, ta có:
\(AO = \sqrt {A{B^2} – B{O^2}} = \sqrt {A{B^2} – {{\left( {\frac{1}{2}BC} \right)}^2}} = \sqrt {{a^2} – {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(AD = 2AO = a\sqrt 3 \Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 3 \)
Vậy độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \) là \(a\sqrt 3 \)