Giải Thực hành 1 Bài 2. Tổng và hiệu của hai vectơ (trang 88, 89, 90) – SGK Toán 10 Chân trời sáng tạo. Tham khảo: Bước 1: Áp dụng quy tắc ba điểm, tìm vectơ \(\overrightarrow a \) và \(\overrightarrow b \.
Câu hỏi/Đề bài:
Cho hình thang ABCD có đáy là AB và CD. Cho biết \(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} ;\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} \). Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.
Hướng dẫn:
Bước 1: Áp dụng quy tắc ba điểm, tìm vectơ \(\overrightarrow a \) và \(\overrightarrow b \)
Bước 2: Xác định hướng của vectơ vừa tìm được
Bước 3: So sánh hướng của 2 vectơ
Lời giải:
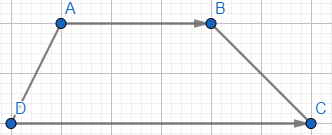
Áp dụng quy tắc ba điểm ta có:
\(\overrightarrow a = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \); \(\overrightarrow b = \overrightarrow {DB} + \overrightarrow {BC} = \overrightarrow {DC} \)
Mà ABCD là hình thang nên AB//DC. Mặt khác vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \) đều có hướng từ trái sang phải, suy ra vectơ \(\overrightarrow {AB} \) và vectơ \(\overrightarrow {DC} \)cùng hướng
Vậy hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng.