Lời giải Hoạt động Khám phá 4 Bài 4. Ba đường conic trong mặt phẳng tọa độ (trang 65, 66, 67) – SGK Toán 10 Chân trời sáng tạo. Gợi ý: Sử dụng phương pháp tọa độ trong mặt phẳng.
Câu hỏi/Đề bài:
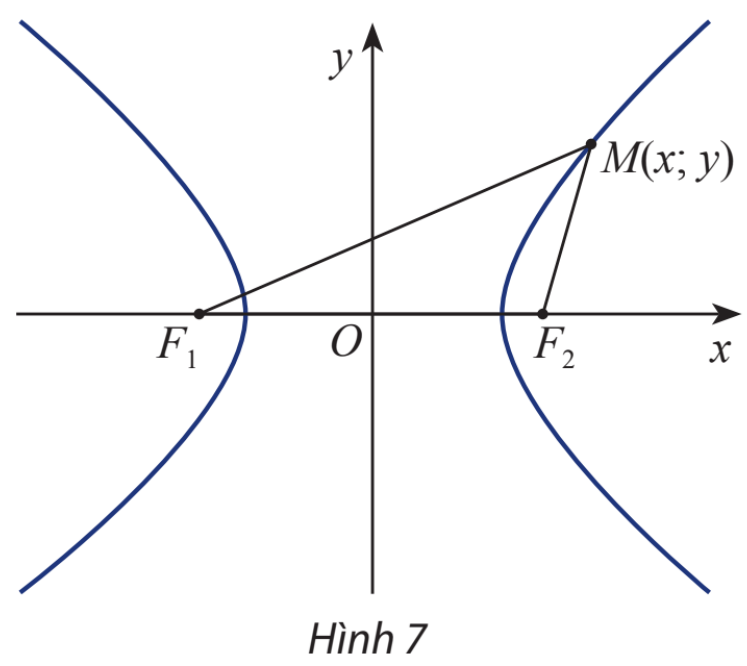
Cho hyperbol (H) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt điểm \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( – c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (H) \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} – \sqrt {{{\left( {x – c} \right)}^2} + {y^2}} } \right| = 2a\)
Hướng dẫn:
Sử dụng phương pháp tọa độ trong mặt phẳng
Lời giải:
a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x – c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x – c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \(\left| {{F_1}M – {F_2}M} \right| = 2a \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} – \sqrt {{{\left( {x – c} \right)}^2} + {y^2}} } \right| = 2a\)