Giải Hoạt động Khám phá 2 Bài 1. Dấu của tam thức bậc hai (trang 8, 9) – SGK Toán 10 Chân trời sáng tạo. Gợi ý: Bước 1: Xác định nghiệm của hàm số là giao của đồ thị và trục hoành.
Câu hỏi/Đề bài:
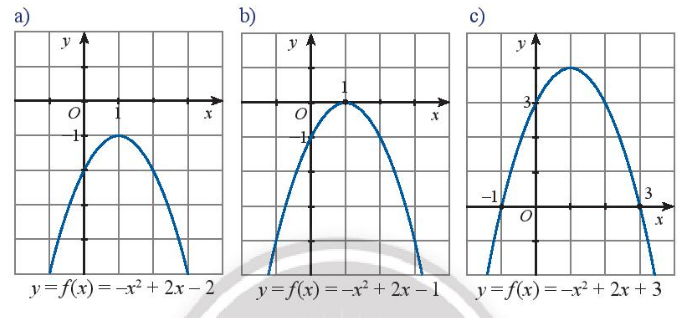
Quan sát đồ thị của các hàm số bậc hai trong các hình thức dưới đây. Trong mỗi trường hợp, hãy cho biết:
+) Các nghiệm (nếu có) và dấu của biệt thức \(\Delta \)
+) Các khoảng giá trị của \(x\)mà trên đó \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\)
Hướng dẫn:
Bước 1: Xác định nghiệm của hàm số là giao của đồ thị và trục hoành
Bước 2: Xác định biệt thức \(\Delta = {b^2} – 4ac\) và xác định dấu của nó
Bước 3: Dựa vào đồ thị xác định dấu của \(f\left( x \right)\)
+) Phần đồ thị nằm trên trục hoành là \(f\left( x \right) > 0\)
+) Phần đồ thị nằm dưới trục hoành là \(f\left( x \right) < 0\)
Lời giải:
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} – 4.\left( { – 1} \right).\left( { – 2} \right) = – 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( – 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} – 4.\left( { – 1} \right).\left( { – 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( – 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = – 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} – 4.\left( { – 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( – 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { – \infty , – 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { – 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { – \infty , – 1} \right) \cup \left( {3, + \infty } \right)\)
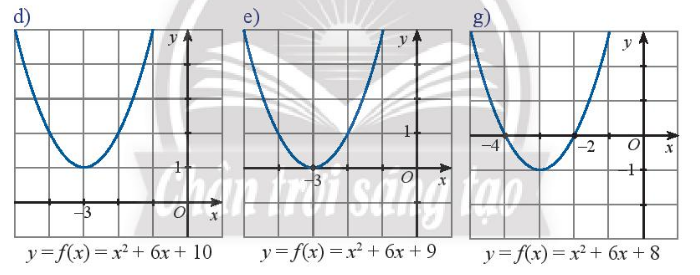
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} – 4.1.10 = – 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = – 3\)
Biệt thức \(\Delta = {6^2} – 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = – 4;{x_2} = – 2\)
Biệt thức \(\Delta = {6^2} – 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { – \infty , – 4} \right) \cup \left( { – 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { – 4, – 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { – \infty , – 4} \right) \cup \left( { – 2, + \infty } \right)\)