Bài 4 trang 10 Toán 10 tập 2 – Chân trời sáng tạo: Xét dấu của các tam thức bậc hai sau đây: a) f x = 2x^2 + 4x + 2

Đề bài/câu hỏi:

Xét dấu của các tam thức bậc hai sau đây:

a) \(f\left( x \right) = 2{x^2} + 4x + 2\)

b) \(f\left( x \right) = – 3{x^2} + 2x + 21\)

c) \(f\left( x \right) = – 2{x^2} + x – 2\)

d) \(f\left( x \right) = – 4x(x + 3) – 9\)

e) \(f\left( x \right) = \left( {2x + 5} \right)\left( {x – 3} \right)\)

Hướng dẫn:

Bước 1: Tính và xác định dấu của biệt thức \(\Delta = {b^2} – 4ac\)

Bước 2: Xác định nghiệm của \(f\left( x \right)\) (nếu có) \(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\)

Bước 3: Xác định dấu của hệ số \(a\)

Bước 4: Xác định dấu của \(f\left( x \right)\)

Lời giải:

a) \(f\left( x \right) = 2{x^2} + 4x + 2\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = – 1\)

và \(a = 2 > 0\)

Ta có bảng xét dấu như sau:

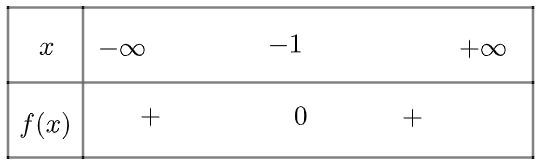
Vậy \(f\left( x \right)\) dương với mọi \(x \ne – 1\)

b) \(f\left( x \right) = – 3{x^2} + 2x + 21\) có \(\Delta = 256 > 0\), hai nghiệm phân biệt là \({x_1} = – \frac{7}{3};{x_2} = 3\)

và \(a = – 3 < 0\)

Ta có bảng xét dấu như sau:

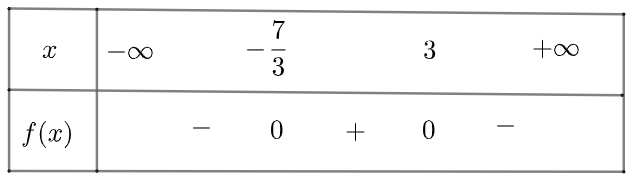
Vậy \(f\left( x \right)\) dương với \(x \in \left( { – \frac{7}{3};3} \right)\) và âm khi \(x \in \left( { – \infty ; – \frac{7}{3}} \right) \cup \left( {3; + \infty } \right)\)

c) \(f\left( x \right) = – 2{x^2} + x – 2\) có \(\Delta = – 15 < 0\), tam thức vô nghiệm

và \(a = – 2 < 0\)

Ta có bảng xét dấu như sau:

Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)

d) \(f\left( x \right) = – 4x\left( {x + 3} \right) – 9 = – 4{x^2} – 12x – 9\) có \(\Delta = 0\), tam thức có nghiệm kép \({x_1} = {x_2} = – \frac{3}{2}\) và \(a = – 4 < 0\)

Ta có bảng xét dấu như sau

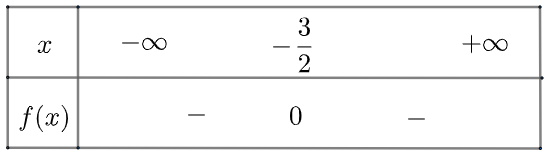
Vậy \(f\left( x \right)\) âm với mọi \(x \ne – \frac{3}{2}\)

e) \(f\left( x \right) = \left( {2x + 5} \right)\left( {x – 3} \right) = 2{x^2} – x – 15\) có \(\Delta = 121 > 0\), có hai nghiệm phân biệt \({x_1} = – \frac{5}{2};{x_2} = 3\) và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

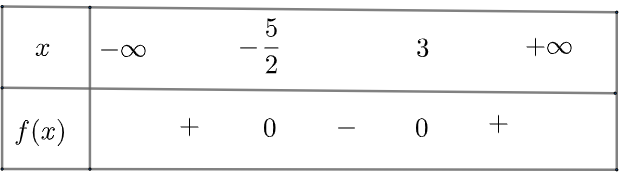
Vậy \(f\left( x \right)\) âm với \(x \in \left( { – \frac{5}{2};3} \right)\) và dương khi \(x \in \left( { – \infty ; – \frac{5}{2}} \right) \cup \left( {3; + \infty } \right)\)