Bước 1: Từ tiêu điểm \( F({p\over 2}; 0)\) viết phương trình chính tắc của parabol có dạng \({y^2} = 2px\) Bước 2. Trả lời Giải bài 15 trang 74 SGK Toán 10 tập 2 – Chân trời sáng tạo – Bài tập cuối Chương 9. Một gương lõm có mặt cắt hình parabol như hình 1, có tiêu điểm cách đỉnh 5 cm….
Đề bài/câu hỏi:
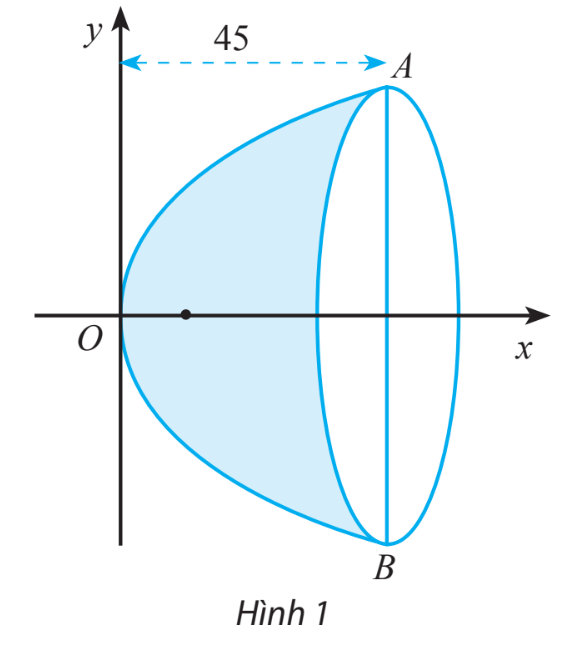
Một gương lõm có mặt cắt hình parabol như hình 1, có tiêu điểm cách đỉnh 5 cm. Cho biết bề sâu của gương là 45 cm. Tính khoảng cách AB
Hướng dẫn:
Bước 1: Từ tiêu điểm \( F({p\over 2}; 0)\) viết phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Bước 2: Thay \(x = 45\) vào phương trình trên tìm \(y_A\)
Bước 3: Xác định khoảng cách \(AB = 2. y_A \)
Lời giải:
Từ giả thiết ta có tiêu điểm \(F(5;0)\), suy ra \(\frac{p}{2} = 5\) hay \(p=10\).
Vậy phương trình chính tắc của parabol là: \({y^2} = 20x\)
Chiều sâu của gương là 45 cm tương ứng với \({x_A} = 45\), thay \({x_A} = 45\) vào phương trình \({y^2} = 20x\) ta có: \({y^2} = 20.45 = 900 \Rightarrow {y_A} = 30 \Rightarrow AB = 2{y_A} = 60 \)
Vậy khoảng cách AB là \(60 cm\)