Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \. Hướng dẫn cách giải/trả lời Giải bài 7 trang 92 SGK Toán 10 tập 2 – Cánh diều – Bài 5. Phương trình đường tròn. Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè….
Đề bài/câu hỏi:
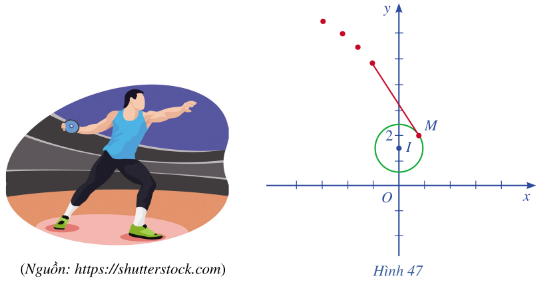
Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè. Khi thực hiện cú ném, vận động viên thường quay lưng lại với hướng ném, sau đó xoay ngược chiều kim đồng hồ một vòng rưỡi của đường tròn để lấy đà rồi thả tay ra khỏi đĩa. Giả sử đĩa chuyển động trên một đường tròn tâm \(I\left( {0;\frac{3}{2}} \right)\) bán kính 0,8 trong mặt phẳng toạ độ Oxy (đơn vị trên hai trục là mét). Đến điểm\(M\left( {\frac{{\sqrt {39} }}{2};2} \right)\), đĩa được ném đi (Hình 47). Trong những giây đầu tiên ngay sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa có phương trình như thế nào?
Hướng dẫn:
Cho điểm (\({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\)) nằm trên đường tròn (C) tâm I(a; b) bán kính R. Gọi \(\Delta \) là tiếp tuyến tại điểm \({M_o}\left( {{x_o};{\rm{ }}{y_o}} \right)\) thuộc đường tròn. Khi đó phương trình tiếp tuyến \(\Delta \) là:
\(\left( {{x_o} – a} \right)\left( {x – {x_o}} \right) + \left( {{y_o} – b} \right)\left( {y – {y_o}} \right) = 0\)
Lời giải:
Sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\begin{array}{l}\left( {\frac{{\sqrt {39} }}{{10}} – 0} \right)\left( {x – \frac{{\sqrt {39} }}{{10}}} \right) + \left( {2 – \frac{3}{2}} \right)\left( {y – 2} \right) = 0\\ \Leftrightarrow \frac{{\sqrt {39} }}{{10}}\left( {x – \frac{{\sqrt {39} }}{{10}}} \right) + \frac{1}{2}\left( {y – 2} \right) = 0\\ \Leftrightarrow \sqrt {39} x + 5y – 13,9 = 0\end{array}\)