Tìm trục đối xứng trên đồ thị, đỉnh I trên đồ thị. b) Đồ thị đi lên thì hàm số đồng biến. Giải và trình bày phương pháp giải Giải bài 4 trang 43 SGK Toán 10 tập 1 – Cánh diều – Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng. Cho đồ thị hàm số bậc hai ở Hình 15….
Đề bài/câu hỏi:
Cho đồ thị hàm số bậc hai ở Hình 15.
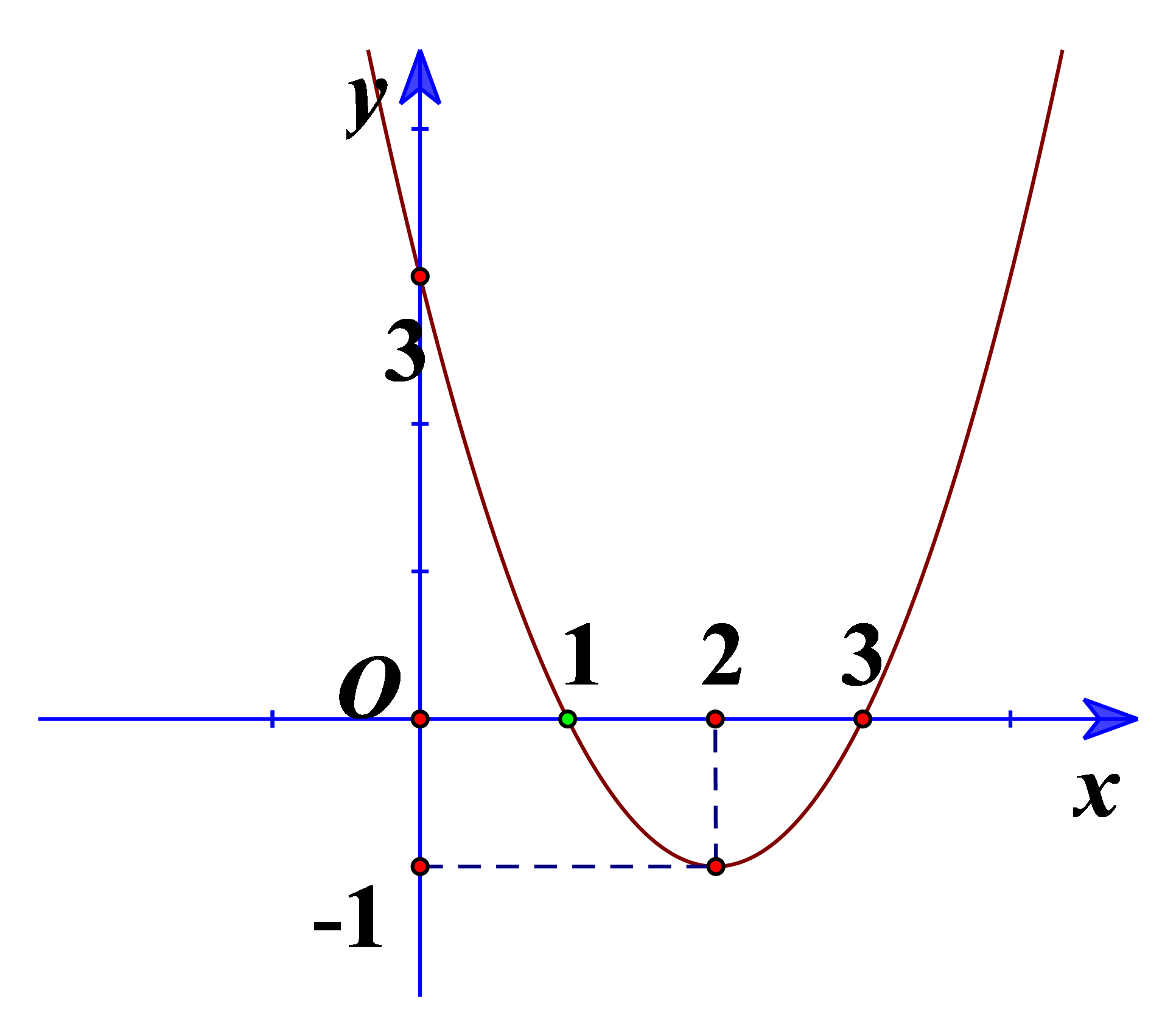
a) Xác định trục đối xứng, tọa độ đỉnh của đồ thị hàm số.
b) Xác định khoảng đồng biến, khoảng nghịch biến của hàm số.
c) Tìm công thức xác định hàm số.
Hướng dẫn:
a) Tìm trục đối xứng trên đồ thị, đỉnh I trên đồ thị.
b) Đồ thị đi lên thì hàm số đồng biến, đi xuống thì hàm số nghịch biến.
c) Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Đồ thị hàm số có đỉnh là \(I\left( {\frac{{ – b}}{{2a}};\frac{{ – \Delta }}{{4a}}} \right)\), xác định thêm 1 điểm thuộc đồ thị và thay vào phương trình tìm a, b, c.
Lời giải:
a) Trục đối xứng là đường thẳng \(x = 2\)
Đỉnh là \(I\left( {2; – 1} \right)\)
b) Từ đồ thị ta thấy trên khoảng \(\left( { – \infty ;2} \right)\) thì hàm số đi xuống nên hàm số nghịch biến trên \(\left( { – \infty ;2} \right)\).
Trên khoảng \(\left( {2; + \infty } \right)\) thì hàm số đi xuống nên đồng biến trên \(\left( {2; + \infty } \right)\).
c) ) Gọi hàm số là \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Đồ thị hàm số có đỉnh là \(I\left( {2; – 1} \right)\) nên ta có:
\(\left\{ \begin{array}{l} – \frac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = – 4a\\4a + 2b + c = – 1\end{array} \right.\)
Ta lại có điểm \(\left( {1;0} \right)\) thuộc đồ thị nên ta có: \(a + b + c = 0\)
Vậy ta có hệ sau:
\(\left\{ \begin{array}{l}b = – 4a\\4a + 2b + c = – 1\\a + b + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = – 4a\\4a + 2.\left( { – 4a} \right) + c = – 1\\a + \left( { – 4a} \right) + c = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = – 4a\\c – 4a = – 1\\c – 3a = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}b = – 4a\\a = 1\\c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = – 4\\a = 1\\c = 3\end{array} \right.\)
Vậy parabol là \(y = {x^2} – 4x + 3\)