Bài 2 trang 79 Toán 10 tập 2 – Cánh diều: Lập phương trình đường thẳng trong các Hình 34, 35, 36, 37

Đề bài/câu hỏi:

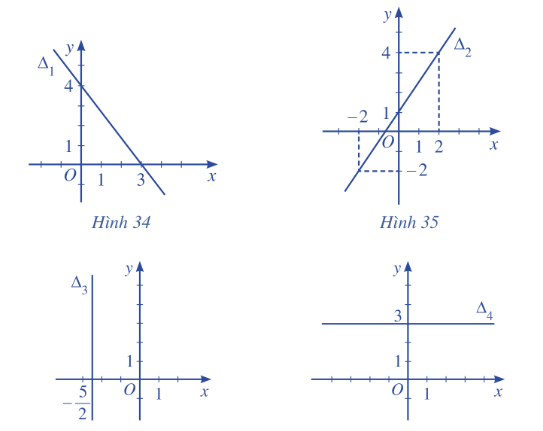
Lập phương trình đường thẳng trong các Hình 34,35,36,37:

Hướng dẫn:

+) Phương trình đoạn chắn của đường thẳng d đi qua hai điểm \(A\left( {a;0} \right),B\left( {0;b} \right)\left( {ab \ne 0} \right)\) có phương trình \(\frac{x}{a} + \frac{y}{b} = 1\)

+) Phương trình đường thằng d đi qua hai điểm \(A\left( {{x_o};{y_o}} \right);B\left( {{x_1};{y_1}} \right)\) là: \(\frac{{x – {x_o}}}{{{x_1} – {x_o}}} = \frac{{y – {y_o}}}{{{y_1} – {y_o}}}\)

+) Phương trình tổng quát của đường thẳng\(\Delta \) đi qua điểm \({M_o}\left( {{x_o};{y_o}} \right)\) và nhận \(\overrightarrow n = \left( {{\rm{a }};{\rm{ b}}} \right)\left( {\overrightarrow n \ne 0} \right)\)làm vecto pháp tuyến là: \(a\left( {x – {x_o}} \right) + b\left( {y – {y_o}} \right) = 0\)

Lời giải:

a) Phương trình đoạn chắn của đường thẳng \({\Delta _1}\) đi qua 2 điểm \(\left( {0;4} \right)\) và \(\left( {3;0} \right)\) là: \(\frac{x}{3} + \frac{y}{4} = 1\)

b) Phương trình đường thẳng \({\Delta _2}\) đi qua 2 điểm \(\left( {2;4} \right)\) và \(\left( { – 2; – 2} \right)\) là:

\(\frac{{x – 2}}{{ – 2 – 2}} = \frac{{y – 4}}{{ – 2 – 4}} \Leftrightarrow \frac{{x – 2}}{{ – 4}} = \frac{{y – 4}}{{ – 6}} \Leftrightarrow 3x – 2y + 2 = 0\)

c) Do đường thẳng \({\Delta _3}\) vuông góc với \({\rm{O}}x\) nên vecto pháp tuyến của \({\Delta _3}\) là: \(\overrightarrow {{n_3}} = \left( {1;0} \right)\)

Vậy phương trình đường thẳng \({\Delta _3}\)đi qua điểm \(\left( { – \frac{5}{2};0} \right)\) có vecto pháp tuyến \(\overrightarrow {{n_3}} = \left( {1;0} \right)\)là: \(1\left( {x + \frac{5}{2}} \right) + 0\left( {y – 0} \right) = 0 \Leftrightarrow x = – \frac{5}{2}\)

d) Do đường thẳng \({\Delta _4}\) vuông góc với \({\rm{O}}x\) nên vecto pháp tuyến của \({\Delta _4}\) là: \(\overrightarrow {{n_4}} = \left( {0;1} \right)\)

Vậy phương trình đường thẳng \({\Delta _4}\) đi qua điểm \(\left( {0;3} \right)\) có vecto pháp tuyến \(\overrightarrow {{n_4}} = \left( {0;1} \right)\)là: \(0\left( {x – 0} \right) + 1\left( {y – 3} \right) = 0 \Leftrightarrow y = 3\)