Phân tích và giải Giải bài 8 trang 75 sách bài tập toán 10 – Chân trời sáng tạo – Bài 2. Định lí côsin và định lí sin. Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB,…
Đề bài/câu hỏi:
Cho tam giác ABC có trọng tâm G. Chứng minh các tam giác GBC, GAB, GAC có diện tích bằng nhau
Lời giải:
Gọi AH, BK, CI là đường cao của tam giác ABC kẻ từ đỉnh A, B, C
GH’, GK’, GI’ là đường cao của tam giác GBC, GAC, GAB kẻ từ G xuống BC, AC, AB
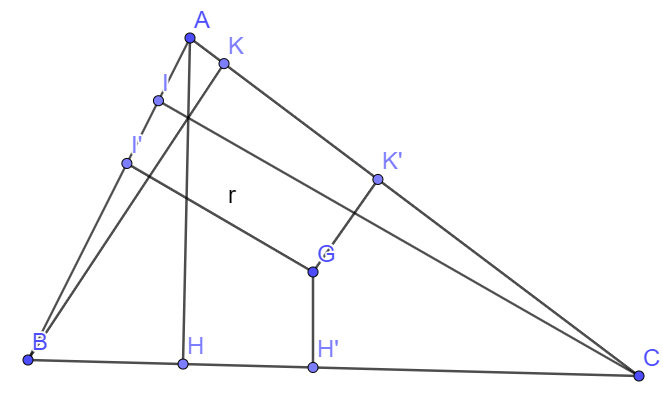
Ta có:
\({S_{GBC}} = \frac{1}{2}BC.GH’;{S_{GAC}} = \frac{1}{2}AC.GK’;{S_{GBA}} = \frac{1}{2}BA.GI’\)
Mà G là trọng tâm của tam giác ABC nên \(GH’ = \frac{1}{3}AH;GK’ = \frac{1}{3}BK;GI’ = \frac{1}{3}CI\)
Suy ra \({S_{GBC}} = \frac{1}{6}BC.AH;{S_{GAC}} = \frac{1}{6}AC.BK;{S_{GBA}} = \frac{1}{6}BA.CI\) (1)
Mặt khác ta có \({S_{ABC}} = \frac{1}{2}BC.AH = \frac{1}{2}AB.CI = \frac{1}{2}AC.BK\) (2)
Từ (1) và (2) ta có \({S_{GBC}} = {S_{GAB}} = {S_{GAC}} = \frac{1}{3}{S_{ABC}}\) (đpcm)