Lời giải bài tập, câu hỏi Giải bài 5 trang 97 sách bài tập toán 10 – Chân trời sáng tạo – Bài 3. Tích của một số với một vectơ. Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB,…
Đề bài/câu hỏi:
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
Lời giải:
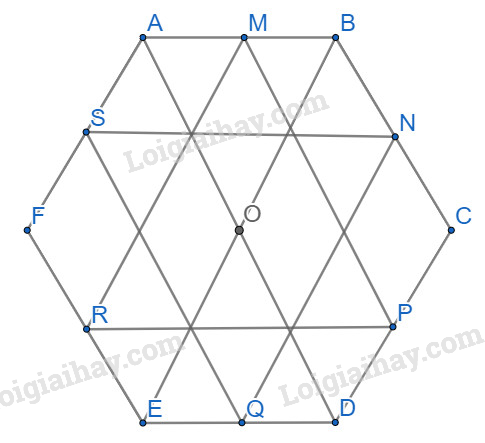
Gọi O là trọng tâm của tam giác MPR
Ta có MN là đường trung bình của tam giác ABC nên \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} \)
Tương tự PQ và RS cũng là đường trung bình của tam giác CDE và EFA nên
\(\overrightarrow {PQ} = \frac{1}{2}\overrightarrow {CE} ;\overrightarrow {RS} = \frac{1}{2}\overrightarrow {EA} \)
Từ đó suy ra \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \frac{1}{2}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {CE} + \frac{1}{2}\overrightarrow {EA} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {CE} + \overrightarrow {EA} } \right) = \overrightarrow 0 \)
\( \Rightarrow \overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RS} = \overrightarrow 0 \)
\( \Leftrightarrow \left( {\overrightarrow {MO} + \overrightarrow {ON} } \right) + \left( {\overrightarrow {PO} + \overrightarrow {OQ} } \right) + \left( {\overrightarrow {RO} + \overrightarrow {OS} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {ON} + \overrightarrow {OQ} + \overrightarrow {OS} = \overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} \)
Mà ta có O là trọng tâm của tam giác MPR nên \(\overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} = \overrightarrow 0 \)
Suy ra \(\overrightarrow {ON} + \overrightarrow {OQ} + \overrightarrow {OS} = \overrightarrow {OM} + \overrightarrow {OP} + \overrightarrow {OR} = \overrightarrow 0 \)
Vậy O vừa trọng tâm của tam giác MPR vừa là trọng tâm của tam giác NQS