Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { – c;0} \right). Giải chi tiết Giải bài 4 trang 76 sách bài tập toán 10 – Chân trời sáng tạo – Bài 4. Ba đường conic trong mặt phẳng tọa độ. Thang leo gợn song cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 100…
Đề bài/câu hỏi:
Thang leo gợn song cho trẻ em trong công viên có hai khung thép cong hình nửa elip cao 100 m và khoảng cách giữa hai chân là 240 cm
a) Hãy chọn hệ tọa độ thích hợp và viết phương trình chính tắc của elip nói trên
b) Tính khoảng cách thẳng đứng từ một điểm cách chân khủng 20 cm lên đến khung thép
Hướng dẫn:
Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { – c;0} \right),{F_2}\left( {c;0} \right)\)và có tiêu cự là \(2c\) với \(c = \sqrt {{a^2} – {b^2}} \)
Lời giải:
a) Gọi phương trình chính tắc của elip là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
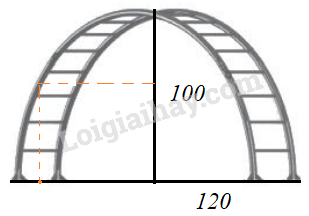
nửa hình elip cao 100 cm \( \Rightarrow b = 100\)
Khoảng cách giữa hai chân là 240 cm \( \Rightarrow 2a = 240 \Leftrightarrow a = 120\)
Vậy phương trình chính tắc của elip là \(\frac{{{x^2}}}{{{{120}^2}}} + \frac{{{y^2}}}{{{{100}^2}}} = 1\)
b)
Điểm cách chân 20 cm có hoành độ là \(\left| x \right| = 120 – 20 = 100\)
Thay vào phương trình ta có:
\(\frac{{{{100}^2}}}{{{{120}^2}}} + \frac{{{y^2}}}{{{{100}^2}}} = 1 \Rightarrow {y^2} = {100^2}\left( {1 – \frac{{{{100}^2}}}{{{{120}^2}}}} \right) \Rightarrow y \approx 55\left( {cm} \right)\)
Vậy khoảng cách thẳng đứng từ điểm đó đến khung thép xấp xỉ 55cm.