Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { – c;0} \right). Phân tích, đưa ra lời giải Giải bài 3 trang 75 SBT toán 10 – Chân trời sáng tạo – Bài 4. Ba đường conic trong mặt phẳng tọa độ. Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 1 m và trục nhỏ là 0,…
Đề bài/câu hỏi:
Để cắt một bảng hiệu quảng cáo hình elip có trục lớn là 1 m và trục nhỏ là 0,6 m từ một tấm ván ép hình chữ nhật có kích thước 1m x 0,6 m, người ta vẽ hình elip đó lên tấm ván ép như hướng dẫn sau:
Chuẩn bị:
– Hai cái đinh, một vòng dây kín không đàn hồi, bút chì
Thực hiện:
– Xác định vị trí (hai tiêu điểm của elip) và ghim hai cái đinh lên hai điểm đó trên tấm ván
– Quàng vòng dây qua hai chiếc đinh và kéo căng tại một điểm M nào đó. Tựa đầu bút chì vào trong vòng dây tại điểm M rồi di chuyển sao cho dây luôn luôn căng. Đầu bút chì vạch lên tấm bìa một người mà người ta gọi là đường eip (Xem hình mình họa trong Hình 10)
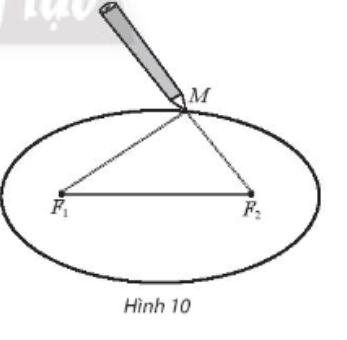
Phải ghim hai cái đinh cách các mép tấm ván ép bao nhiêu và lấy vòng dây có độ dài là bao nhiêu?
Hướng dẫn:
Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\) có hai tiêu điểm \({F_1}\left( { – c;0} \right),{F_2}\left( {c;0} \right)\)và có tiêu cự là \(2c\) với \(c = \sqrt {{a^2} – {b^2}} \)
Lời giải:
Phương trình Elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\)
Ta có: \(2a = 1m = 100cm;2b = 0,6m = 60cm\)
\( \Rightarrow {c^2} = {a^2} – {b^2} = {50^2} – {30^2} = 1600 \Rightarrow c = 40\)
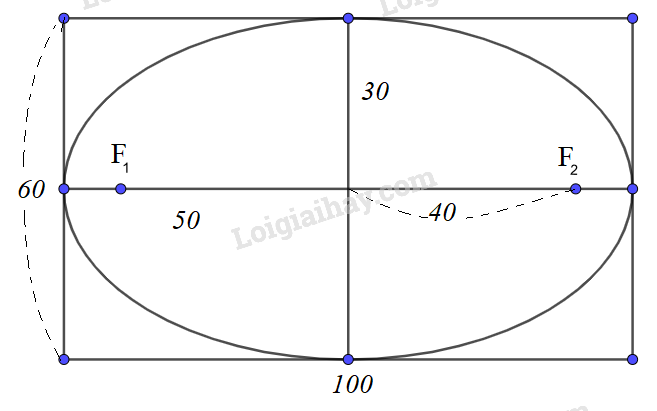
+ Ta có \(a – c = 10\left( {cm} \right)\)
=> cần ghim hai cái đinh cách các mép tấm ván ép 10 cm.
vòng dây dài \(M{F_1} + M{F_2} + {F_1}{F_2} = 2a + 2c = 180\left( {cm} \right)\)
Vậy phải ghim hai cái đinh cách các mép tấm ván ép 10 cm và lấy vòng dây độ dài là 180 cm hay 1,8 m