Trả lời Giải bài 10 trang 23 SBT toán 10 – Chân trời sáng tạo – Bài tập cuối Chương 7. Cho tam giác ABC và ABD cùng vuông tại A như hình 3 có \(AB = x;BC = 5\…
Đề bài/câu hỏi:
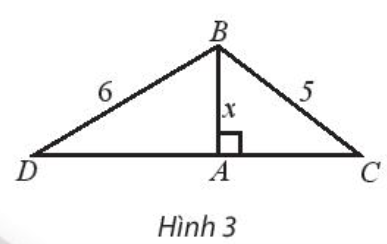
Cho tam giác ABC và ABD cùng vuông tại A như hình 3 có \(AB = x;BC = 5\) và \(BD = 6\)
a) Biểu diễn độ dài cạnh AC và AD theo x
b) Tìm x để chu vi của tam giác ABC là 12
c) Tìm x để \(AD = 2AC\)
Lời giải:
a) Áp dụng định lí pitago cho tam giác ABC ta có:
\(AC = \sqrt {B{C^2} – A{B^2}} = \sqrt {{5^2} – {x^2}} = \sqrt {25 – {x^2}} \)
Áp dụng định lí pitago cho tam giác ABD ta có:
\(AD = \sqrt {B{D^2} – A{B^2}} = \sqrt {{6^2} – {x^2}} = \sqrt {36 – {x^2}} \)
b) Ta có: \(AB + AC + BC = 12\)
\(\begin{array}{l} \Leftrightarrow x + \sqrt {25 – {x^2}} + 5 = 12\\ \Leftrightarrow \sqrt {25 – {x^2}} = 7 – x\\ \Rightarrow 25 – {x^2} = 49 – 14x + {x^2}\\ \Rightarrow 2{x^2} – 14x + 24 = 0\end{array}\)
\( \Rightarrow x = 3\) hoặc \(x = 4\)
Thay hai giá trị vừa tìm được vào phương trình ban đầu ta thấy cả hai giá trị đều thỏa mãn
Vậy khi \(x = 3\) hoặc \(x = 4\) thì chu vi của tam giác ABC là 12
c) Ta có: \(AD = 2AC\)
\(\begin{array}{l} \Leftrightarrow \sqrt {36 – {x^2}} = 2\sqrt {25 – {x^2}} \\ \Rightarrow 36 – {x^2} = 4\left( {25 – {x^2}} \right)\\ \Rightarrow 3{x^2} – 64 = 0\end{array}\)
\( \Rightarrow x = – \frac{{8\sqrt 3 }}{3}\) (loại vì \(x > 0\)) hoặc \(x = \frac{{8\sqrt 3 }}{3}\)
Thay \(x = \frac{{8\sqrt 3 }}{3}\) vào phương trình ban đầu ta thấy thỏa mãn
Vậy \(x = \frac{{8\sqrt 3 }}{3}\) thì \(AD = 2AC\)