Bước 1: Biểu diễn độ dài DB (hoặc DC) theo DC (hoặc DB) và xác định hướng các vectơ tương ứng Bước 2. Trả lời Giải bài 53 trang 100 SBT toán 10 – Cánh diều – Bài 5. Tích của một số với một vectơ. Cho tam giác ABC, kẻ phân giác AD. Đặt AB = c, AC = b. Chứng minh:…
Đề bài/câu hỏi:
Cho tam giác ABC, kẻ phân giác AD. Đặt AB = c, AC = b. Chứng minh:
\(b\overrightarrow {DB} + c\overrightarrow {DC} = \overrightarrow 0 \) (*)
Hướng dẫn:
Bước 1: Biểu diễn độ dài DB (hoặc DC) theo DC (hoặc DB) và xác định hướng các vectơ tương ứng
Bước 2: Sử dụng định lí đường phân giác trong tam giác để biến đổi tỉ số độ dài \(\frac{{DB}}{{DC}}\)
Bước 3: Biến đổi đẳng thức ở bước 1 rồi kết luận
Lời giải:
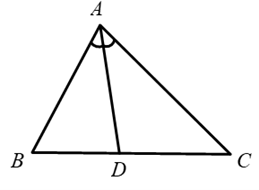
Ta có: \(DB = \frac{{DB}}{{DC}}.DC\) mà \(\overrightarrow {DB} \) và \(\overrightarrow {DC} \) ngược hướng
\( \Rightarrow \overrightarrow {DB} = – \frac{{DB}}{{DC}}.\overrightarrow {DC} \)(1)
Theo giả thiết, AD là đường phân giác của ∆ABC
\( \Rightarrow \frac{{AB}}{{AC}} = \frac{{DB}}{{DC}} = \frac{c}{b}\) (2)
Từ (1) và (2) suy ra \(\overrightarrow {DB} = – \frac{c}{b}.\overrightarrow {DC} \Leftrightarrow b\overrightarrow {DB} = – c\overrightarrow {DC} \Leftrightarrow b\overrightarrow {DB} + c\overrightarrow {DC} = \overrightarrow 0 \) (ĐPCM)