Bước 1: Xác định hướng và độ lớn các vectơ (sử dụng các quy tắc cộng, trừ, quy tắc hình bình hành, …) Bước 2. Hướng dẫn trả lời Giải bài 52 trang 100 SBT toán 10 – Cánh diều – Bài 5. Tích của một số với một vectơ. Cho tam giác ABC. Xác định các điểm M, N, P trong môi trường hợp sau:…
Đề bài/câu hỏi:
Cho tam giác ABC. Xác định các điểm M, N, P trong môi trường hợp sau:
a) \(\overrightarrow {AM} = \overrightarrow {CB} \)
b) \(\overrightarrow {AN} = – \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
c) \(\overrightarrow {PA} – \overrightarrow {PB} + 2\overrightarrow {PC} = \overrightarrow 0 \)
Hướng dẫn:
Bước 1: Xác định hướng và độ lớn các vectơ (sử dụng các quy tắc cộng, trừ, quy tắc hình bình hành,…)
Bước 2: Xác định vị trí các điểm M, N, P dựa vào hướng và độ lớn các vectơ tương ứng rồi kết luận
Lời giải:
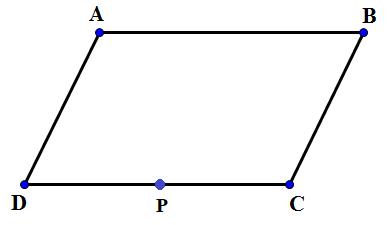
a) Theo giả thiết, \(\overrightarrow {AM} = \overrightarrow {CB} \)\( \Rightarrow \) \(\overrightarrow {AM} \) cùng hướng và có độ lớn bằng \(\overrightarrow {CB} \)
Vậy điểm M thuộc đường thẳng đi qua A, song song với BC sao cho AMBC là hình bình hành
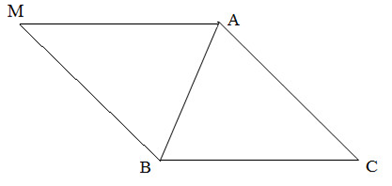
b) Theo giả thiết, \(\overrightarrow {AN} = – \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)
Dựng hình bình hành ABDC, theo quy tắc hình bình hành ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)\( \Rightarrow \overrightarrow {AN} = – \frac{1}{2}\overrightarrow {AD} \)
Vậy điểm N thuộc tia đối của tia AD thỏa mãn \(AN = \frac{1}{2}AD\)
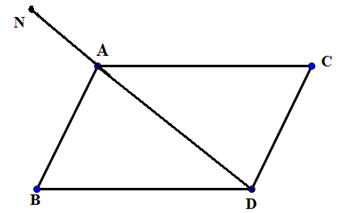
c) Theo giả thiết, \(\overrightarrow {PA} – \overrightarrow {PB} + 2\overrightarrow {PC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + 2\overrightarrow {PC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {PC} = – \frac{1}{2}\overrightarrow {BA} \)
Dựng hình bình hành ABCD. Khi đó P là trung điểm của CD
Vậy điểm P là trung điểm đoạn thẳng CD thỏa mãn ABCD là hình bình hành