Bước 1: Dựng hình bình hành ABDC Bước 2: Sử dụng quy tắc trừ hai vectơ và quy tắc hình bình hành để biến đổi. Lời giải bài tập, câu hỏi Giải bài 40 trang 92 SBT toán 10 – Cánh diều – Bài 4. Tổng và hiệu của hai vectơ. Cho tam giác ABC thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} – \overrightarrow…
Đề bài/câu hỏi:
Cho tam giác ABC thỏa mãn \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AC} } \right|\) (*). Chứng minh tam giác ABC vuông tại A.
Hướng dẫn:
Bước 1: Dựng hình bình hành ABDC
Bước 2: Sử dụng quy tắc trừ hai vectơ và quy tắc hình bình hành để biến đổi giả thiết (*)
Bước 3: Sử dụng dấu hiệu nhận biết hình chữ nhật để chứng minh tam giác ABC vuông tại A
Lời giải:
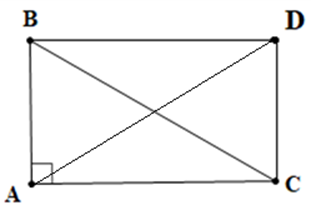
Dựng hình bình hành ABDC. Khi đó \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AB} – \overrightarrow {AC} } \right| \Leftrightarrow \left| {\overrightarrow {AD} } \right| = \left| {\overrightarrow {CB} } \right| \Leftrightarrow AD = BC\)
\( \Rightarrow \) Hình bình hành ABCD có hai đường chéo bằng nhau nên là hình chữ nhật
\( \Rightarrow \widehat {BAC} = {90^0}\). Vậy tam giác ABC vuông tại A (ĐPCM)