Bài 2 trang 42 SBT toán 10 – Cánh diều: Cho đồ thị hàm số y = f x ở Hình 4. Phát biểu nào sau đây là đúng? A

Đề bài/câu hỏi:

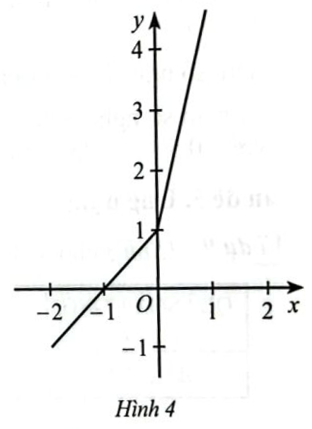
Cho đồ thị hàm số \(y = f\left( x \right)\) ở Hình 4. Phát biểu nào sau đây là đúng?

A. Đồ thị hàm số cắt trục hoành tại điểm của hoành độ bằng 1

B. Đồ thị hàm số cắt trục tung tại điểm có tung bộ bằng -1

C. Hàm số đồng biến trên khoảng \(\left( { – 1; + \infty } \right)\), ngịch biến trên khoảng \(\left( { – \infty ; – 1} \right)\)

D. Hàm số đồng biến trên \(\mathbb{R}\)

Hướng dẫn:

Hàm số \(f\left( x \right)\) đồng biến trên \(\left( {a;b} \right)\) khi \(\forall {x_1},{x_2} \in \left( {a;b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)

Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( {a;b} \right)\) khi \(\forall {x_1},{x_2} \in \left( {a;b} \right),{x_1} f\left( {{x_2}} \right)\)

Lời giải:

Đồ thị hàm số cắt trục hoành tại điểm có tọa độ (-1;0) => A sai

Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0;1) => B sai

Quan sát đồ thị, ta thấy: Đồ thị hàm số đi lên từ trái sang phải => Hàm số đồng biến trên \(\mathbb{R}\)

Chọn D.