Gắn hệ trục tọa độ cho cổng parabol, lập phương trình parabol thể hiện cổng. Gợi ý giải Giải bài 19 trang 48 SBT toán 10 – Cánh diều – Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng. Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao…
Đề bài/câu hỏi:
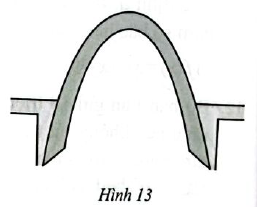
Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m. Từ một điểm M trên thân cổng người ta đo được khoảng cách tới mặt đất là MK = 1,6 m và khoảng cách từ K tới chân cổng gần nhất là BK = 0,5 m. Tính chiều cao của cổng theo đơn vị mét (làm tròn kết quả đến hàng phần mười)
Hướng dẫn:
Gắn hệ trục tọa độ cho cổng parabol, lập phương trình parabol thể hiện cổng
Lời giải:
Lấy hệ trục tọa độ \(Oxy\) sao cho vị trí điểm B trùng với gốc O, trục \(Ox\) nằm trên đường nối chân hai cổng, C nằm trên tia \(Ox\) (đơn vị trên các trục tính theo mét)
Khi đó tổng ra vào là một phần của đồ thị hàm số \(y = \frac{{ – 32}}{{85}}{x^2} + \frac{{288}}{{85}}x\)
Đỉnh của đồ thị hàm số trên có tung độ là 7,6
Vậy chiều cao của cổng là 7,6 m.