Bài 18 trang 48 SBT toán 10 – Cánh diều: Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b

Đề bài/câu hỏi:

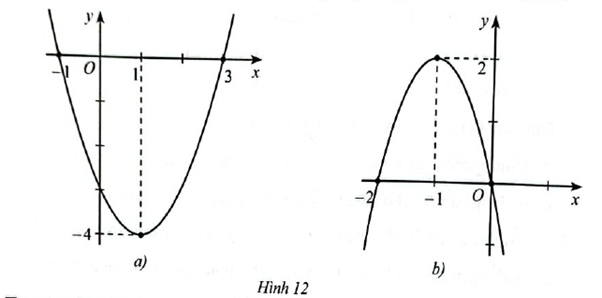
Xác định hàm số bậc hai biết đồ thị tương ứng trong mỗi Hình 12a, 12b:

Hướng dẫn:

Xác định các hệ số a, b, c qua các đỉnh và các điểm thuộc parabol trong đồ thị đã cho

Lời giải:

Gọi hàm số bậc hai cần tìm là \(y = f\left( x \right) = a{x^2} + bx + c\)

a) Đồ thị hàm số có đỉnh là \(I\left( {1; – 4} \right)\) và đi qua điểm \(\left( { – 1;0} \right),\left( {3;0} \right)\), suy ra:\(\left\{ \begin{array}{l}x = \frac{{ – b}}{{2a}} = 1\\a{\left( { – 1} \right)^2} + b\left( { – 1} \right) + c = 0\\a{.3^2} + b.3 + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = – 2a\\a – b + c = 0\\9a + 3b + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 1\\b = – 2\\c = – 3\end{array} \right.\)

Vậy parabol đó là \(y = {x^2} – 2x – 3\)

b) Đồ thị hàm số có đỉnh là \(I\left( { – 1;2} \right)\) và đi qua điểm \(\left( {0;0} \right),\left( { – 2;0} \right)\), suy ra:\(\left\{ \begin{array}{l}x = \frac{{ – b}}{{2a}} = – 1\\a{.0^2} + b.0 + c = 0\\a.{\left( { – 2} \right)^2} + b.\left( { – 2} \right) + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 2a\\c = 0\\4a – 2b + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = – 2\\b = – 4\\c = 0\end{array} \right.\)

Vậy parabol đó là \(y = – 2{x^2} – 4x\)