Trả lời Giải đề 8 Tổng hợp 10 đề thi học kì 1 Toán 10 kết nối tri thức – Đề thi đề kiểm tra Toán lớp 10 Kết nối tri thức.
Câu hỏi/Đề bài:
HƯỚNG DẪN GIẢI CHI TIẾT
I. Phần trắc nghiệm (5 điểm – 25 câu)
|
1.C |
2.B |
3.B |
4.C |
5.B |
6.B |
7.C |
8.A |
9.A |
10.A |
|
11.C |
12.A |
13.B |
14.A |
15.C |
16.B |
17.D |
18.A |
19.C |
20.B |
|
21.B |
22.A |
23.B |
24.D |
25.C |
|||||
Câu 1 (NB):
Hướng dẫn:
Mệnh đề chứa biến là mệnh đề có biến số
Cách giải:
x + y > 0 là mệnh đề chứa biến
Chọn C.
Câu 2 (NB):
Hướng dẫn:
Mệnh đề chứa biến sai khi có ít nhất 1 giá trị của biến sai.
Cách giải:
sai khi x = 1, đúng do có 1 giá trị x = 1 thỏa mãn.
Chọn B.
Câu 3 (NB):
Hướng dẫn:
phương trình và đối chiếu điều kiện \(x \in \mathbb{Z}\).
Cách giải:
\(9{x^2} – 8x – 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \mathbb{Z}\\x = \frac{{ – 1}}{9} \notin \mathbb{Z}\end{array} \right.\). Suy ra \(X = \left\{ 1 \right\}\)
Chọn B
Câu 4 (NB):
Hướng dẫn:
Tìm giao 2 tập hợp ta tìm phần tử chung của hai tập hợp đó.
Cách giải:
\(X \cap Y\)=\(\left\{ {4;7} \right\}\)
Chọn C.
Câu 5 (TH):
Hướng dẫn:
Thể hiện các tập hợp trên trục số và tìm hợp của chúng
Cách giải:
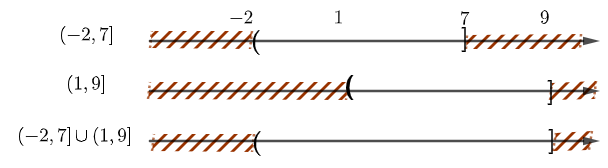
Chọn B.
Câu 6 (VD):
Hướng dẫn:
\(A \subset B\) khi mọi phần tử của A đều là phần tử của B.
Cách giải:
\(A \subset B \Leftrightarrow \left\{ \begin{array}{l}m \ge – 1\\m + 2 \le 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge – 1\\m \le 0\end{array} \right. \Leftrightarrow – 1 \le m \le 0\)
Chọn B
Câu 7 (NB):
Hướng dẫn:
Thay tọa độ x, y vào bât phương trình và kiểm tra tính đúng sai.
Cách giải:
Vì 2.0 + 1 = 1 không nhỏ hơn 1 nên \(\left( {0;1} \right)\) không thuộc miền nghiệm của bất phương trình.
Chọn C.
Câu 8 (NB):
Hướng dẫn:
Chọn 2 điểm bất kì thuộc hoặc không thuộc miền nghiệm để kiểm tra đáp án. Thông thường ta hay chọn gốc tọa độ O(0,0).
Cách giải:
Vì điểm (0,0) và (3,0) thuộc miền nghiệm nên hình vẽ A đúng.
Chọn A.
Câu 9 (NB):
Hướng dẫn:
Tần suất \({f_i} = \frac{n}{N} \Rightarrow n = {f_i}.N\)
Cách giải:
\(n = {f_i}.N = 2,5\% .400 = 10\)
Chọn A.
Câu 10 (NB):
Hướng dẫn:
Biểu đồ hình quạt thích hợp nhất để thể hiện bảng phân bố tần suất.
Cách giải:
Biểu đồ hình quạt thích hợp nhất để thể hiện bảng phân bố tần suất.
Chọn A.
Câu 11 (NB):
Hướng dẫn:
Số trung bình là \(\overline x = \frac{{{x_1} + {x_2} + {x_3} + … + {x_n}}}{n}\)
Cách giải:
\(\overline x = \frac{{{x_1} + {x_2} + {x_3} + … + {x_n}}}{n} = \frac{{21 + 23 + 24 + 25 + 22 + 20}}{6} = 22.5\)
Chọn C.
Câu 12 (TH):
Hướng dẫn:
Tần suất \({f_i} = \frac{n}{N} \Rightarrow n = {f_i}.N\)
Cách giải:
Tần suất của số 4 là \(f = \frac{{10}}{{50}} = \frac{1}{5} = 20\% \)
Chọn A.
Câu 13 (TH):
Hướng dẫn:
Dùng MTCT để tính
Cách giải:
Chọn B.
Câu 14 (TH):
Hướng dẫn:
Dùng MTCT để tính
Cách giải:
Chọn A.
Câu 15 (TH):
Hướng dẫn:
Hai góc \(\alpha \) và \(\beta \) bù nhau thì \(\sin \alpha = \sin \beta \); \(\cos \alpha = – \cos \beta \).
Cách giải:
Giả sử \(\hat A = \alpha ;\hat B + \hat C = \beta \). Biểu thức trở thành \(P = \cos \alpha \cos \beta – \sin \alpha \sin \beta \).
Trong tam giác ABC có \(\hat A + \hat B + \hat C = {180^^\circ } \Rightarrow \alpha + \beta = {180^^\circ }\).
Do hai góc \(\alpha \) và \(\beta \) bù nhau nên \(\sin \alpha = \sin \beta \); \(\cos \alpha = – \cos \beta \).
Do đó \(P = \cos \alpha \cos \beta – \sin \alpha \sin \beta = – {\cos ^2}\alpha – {\sin ^2}\alpha = – \left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) = – 1\).
Chọn C.
Câu 16 (NB):
Hướng dẫn:
Dùng định lý sin trong tam giác.
Cách giải:
Chọn B.
Câu 17 (TH):
Hướng dẫn:
Dùng định lý cosin \({b^2} = {a^2} + {c^2} – 2ac.\cos B\)
Cách giải:
\({b^2} = {a^2} + {c^2} – 2ac.\cos B = {5^2} + {3^2} – 2.3.8.\cos 60 = 19 \Rightarrow b = \sqrt {19} \)
Chọn D.
Câu 18 (VD):
Hướng dẫn:
Chia hình thoi thành 2 tam giác bằng nhau và áp dụng công thức diện tích tam giác.
Cách giải:
\({S_{\Delta ABD}} = \frac{1}{2}.AB.AD.\sin A = \frac{1}{2}.a.a.\sin 30 = \frac{{{a^2}}}{4}\)
Chọn A.
Câu 19 (VD):
Hướng dẫn:
Chia cả tử và mẫu của phân thức cho cos x để xuất hiện tan x.
Cách giải:
\(E = \frac{{2\cos \alpha – 3\sin \alpha }}{{3\cos \alpha – \sin \alpha }} = \frac{{2.\frac{{\cos \alpha }}{{\cos \alpha }} – 3.\frac{{\sin \alpha }}{{\cos \alpha }}}}{{3.\frac{{\cos \alpha }}{{\cos \alpha }} – \frac{{\sin \alpha }}{{\cos \alpha }}}} = \frac{{2 – 3\tan x}}{{3 – \tan x}} = \frac{{17}}{8}\)
Chọn C.
Câu 20 (TH):
Hướng dẫn:
Dùng quy tắc cộng, quy tắc trừ và quy tắc hình bình hành.
Cách giải:
Theo quy tắc cộng \(\overrightarrow {MP} + \overrightarrow {NM} = \overrightarrow {NM} + \overrightarrow {MP} = \overrightarrow {NP} \)
Chọn B.
Câu 21 (NB):
Hướng dẫn:
Hai vecto đối nhau khi chúng cùng phương và ngược hướng.
Cách giải:
Chọn B.
Câu 22 (TH):
Hướng dẫn:
Hai veto bằng nhau khi chúng cùng phương và cùng hướng
Phân biệt giữa vecto và độ dài vecto
Cách giải:
\(\overrightarrow {AB} = \overrightarrow {AC} \)sai do 2 vecto này không cùng phương
Chọn A.
Câu 23 (TH):
Hướng dẫn:
Dùng tính chất trọng tâm tam giác
Cách giải:
Gọi \(G\) là trọng tâm tam giác \(ABC\).
Ta có \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0 \Rightarrow M \equiv G\).
Chọn B.
Câu 24 (TH):
Hướng dẫn:
Dùng công thức tích vô hướng của 2 vecto
Cách giải:
\(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|\cos \left( {\overrightarrow {AC} ,\,\overrightarrow {CB} } \right) = a.a.\cos 120 = \frac{{ – {a^2}}}{2}\)
Chọn D.
Câu 25 (VD):
Hướng dẫn:
Dùng công thức tích vô hướng của 2 vecto
Cách giải:
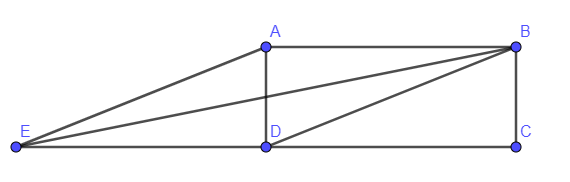
\(B{D^2} = A{B^2} + A{C^2} = {5^2} + {8^2} = 89 \Rightarrow BD = \sqrt {89} \)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {BD} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {BD} } \right|.\cos \left( {\overrightarrow {AB} ,\,\overrightarrow {BD} } \right) = 8.\sqrt {89} .\cos BAE\\ = 8.\sqrt {89} .\frac{{A{B^2} + A{E^2} – B{E^2}}}{{2AB.AE}} = 8.\sqrt {89} .\frac{{{8^2} + 89 – 125}}{{2.8.\sqrt {89} }} = 14\end{array}\)
Chọn C.
II. Phần tự luận (5 điểm)
Câu 1 (TH):
Hướng dẫn:
Dùng định nghĩa các phép toán trên tập hợp.
Cách giải:
a. \(S = \left\{ {1;2;3;4} \right\},T = \left\{ {2;4;6} \right\}\)
\(S \cap T = \left\{ {2,4} \right\},\,S \cup T = \left\{ {1,2,3,4,6} \right\},\,\,S\backslash T = \left\{ {1,3} \right\}\)
b. \(\mathop C\nolimits_\mathbb{R} B = \mathbb{R}\backslash \left[ {4 – 3m; + \infty } \right) = \left( { – \infty ,\,4 – 3m} \right)\)
Để \(\mathop C\nolimits_\mathbb{R} B \subset A\) tức là \(\left( { – \infty ,\,4 – 3m} \right) \subset \left( { – \infty ;2023} \right) \Leftrightarrow 4 – 3m \le 2023 \Leftrightarrow m \ge 673\).
Câu 2 (VD):
Hướng dẫn:
Dùng các hệ thức lượng trong tam giác.
Cách giải:
\(BC = DC.\tan 23,{6^0} = 200.\tan 23,{6^0} \approx 87,378\)m
\(\angle ADC = \angle ADB + \angle BDC = 15,9 + 23,6 = 39,5\)
\(AC = DC.\tan ADC = 200.\tan 39,{5^0} = 164,867m\)
Vậy chiều cao tháp là AB = AC – BC = 164,867 – 87,378 =77,489 m
Câu 3 (VD):
Hướng dẫn:
Dùng quy tắc cộng, chèn điểm, các vecto bằng nhau.
Cách giải:
a. \(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {BA} + \overrightarrow {MC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MC} = \overrightarrow {AB} \)
Suy ra MABC là hình bình hành.
b. Ta có \(\left| {\overrightarrow {MB} – \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} – \overrightarrow {BA} } \right| \Leftrightarrow \left| {\overrightarrow {CB} } \right| = \left| {\overrightarrow {AM} } \right| \Rightarrow AM = BC\)
Mà \(A,\;B,\;C\) cố định nên tập hợp điểm \(M\) là đường tròn tâm \(A\), bán kính \(BC\).