Trả lời Đề 8 Tổng hợp 10 đề thi học kì 1 Toán 10 kết nối tri thức – Đề thi đề kiểm tra Toán lớp 10 Kết nối tri thức.
Câu hỏi/Đề bài:
I. Phần trắc nghiệm (5 điểm – 25 câu)
Câu 1: Trong các câu sau đâu là mệnh đề chứa biến?
A. 2 là số nguyên tố. B. 17 là số chẵn
C. x + y > 0 D. Hình vuông có hai đường chéo vuông góc
Câu 2: Cho mệnh đề ,. Xét tính đúng sai của hai mệnh đề P, Q.
A. P đúng, Q sai B. P sai, Q đúng C. P, Q đều đúng D. P, Q đều sai
Câu 3: Liệt kê các phần tử của phần tử tập hợp \(X = \left\{ {x \in \mathbb{Z}|9{x^2} – 8x – 1 = 0} \right\}\).
A. \(X = \left\{ 0 \right\}\) B. \(X = \left\{ 1 \right\}\) C. \(X = \left\{ {\frac{3}{2}} \right\}\) D. \(X = \left\{ {1;\frac{3}{2}} \right\}\)
Câu 4: Cho \(X = \left\{ {7;2;8;4;9;12} \right\}\);\(Y = \left\{ {1;3;7;4} \right\}\). Tập nào sau đây bằng tập \(X \cap Y\)?
A. \(\left\{ {1;2;3;4;8;9;7;12} \right\}\) B. \(\left\{ {2;8;9;12} \right\}\) C. \(\left\{ {4;7} \right\}\) D. \(\left\{ {1;3} \right\}\)
Câu 5: Cho hai tập hợp \(A = \left[ { – 2;7} \right),B = \left( {1;9} \right]\). Tìm \(A \cup B\).
A. \(\left( {1;7} \right)\) B. \(\left[ { – 2;9} \right]\) C. \(\left[ { – 2;1} \right)\) D. \(\left( {7;9} \right]\)
Câu 6: Cho tập hợp \(A = \left[ {m;m + 2} \right],B\left[ { – 1;2} \right]\). Tìm điều kiện của m để \(A \subset B\).
A. \(m \le – 1\) hoặc \(m \ge 0\) B. \( – 1 \le m \le 0\) C. \(1 \le m \le 2\) D. \(m 2\)
Câu 7: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình \(2x + y < 1\)
A. \(\left( { – 2;1} \right)\) B. \(\left( {3; – 7} \right)\) C. \(\left( {0;1} \right)\) D. \(\left( {0;0} \right)\)
Câu 8: Miền nghiệm của bất phương trình \(3x + 2y > – 6\) là
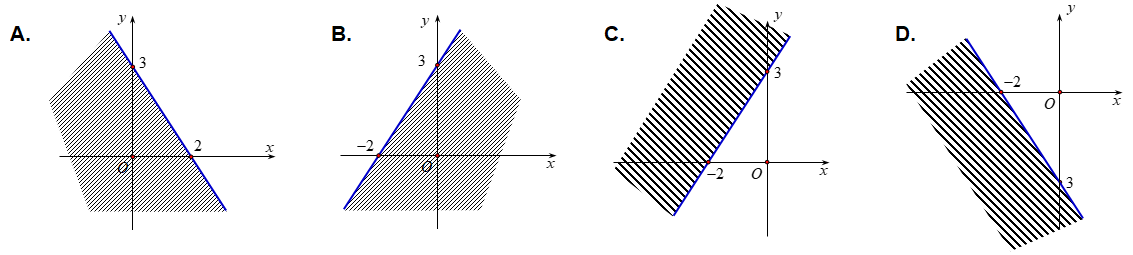
Câu 9: Thống kê điểm thi môn toán trong một kì thi của 400 em học sinh . Người ta thấy số bài được điểm 10 chiếm tỉ lệ 2,5 %. Hỏi tần số của giá trị xi = 10 là bao nhiêu?
A. 10 B. 20 C. 25 D. 5
Câu 10: Trong các loại biểu đồ sau, loại biểu đồ nào thích hợp nhất cho việc thể hiện bảng phân bố tần suất.
A. Biểu đồ hình quạt B. Biểu đồ hình cột
C. Biểu đồ hình cột kép D. Biểu đồ đa giác tần số
Câu 11: Cho dãy số liệu thống kê: 21,23,24,25,22,20. Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 23.5 B. 22 C. 22.5 D. 14
Câu 12: Cho bảng phân bố tần số sau :
|
xi |
1 |
2 |
3 |
4 |
5 |
6 |
Cộng |
|
ni |
10 |
5 |
15 |
10 |
5 |
5 |
50 |
Mệnh đề đúng là :
A. Tần suất của số 4 là 20% B. Tần suất của số 2 là 20%
C. Tần suất của số 5 là 45 D. Tần suất của số 5 là 90%
Câu 13: Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán
|
Điểm |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Cộng |
|
Số học sinh |
2 |
3 |
7 |
18 |
3 |
2 |
4 |
1 |
40 |
Số trung vị là?
A. 5 B. 6 C. 6,5 D. 7
Câu 14: Cho bảng số liệu ghi lại điểm của 40 học sinh trong bài kiểm tra 1 tiết môn toán
|
Điểm |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Cộng |
|
Số học sinh |
2 |
3 |
7 |
18 |
3 |
2 |
4 |
1 |
40 |
Độ lệch chuẩn là:
A. 1,577 B. 2.553 C. 2,49 D. 6,1
Câu 15: Cho tam giác \(ABC\). Tính \(P = \cos A.\cos \left( {B + C} \right) – \sin A.\sin \left( {B + C} \right)\).
A. \(P = 0.\) B. \(P = 1.\) C. \(P = – 1.\) D. \(P = 2.\)
Câu 16: Cho tam giác \(ABC\). Tìm công thức sai:
A. \(\frac{a}{{\sin A}} = 2R\,.\) B. \(\sin A = \frac{a}{{2R}}\,.\) C. \(b\sin B = 2R\,.\) D. \(\sin C = \frac{{c\sin A}}{a}\,.\)
Câu 17: Tam giác \(ABC\) có \(a = 5,c = 3,\widehat B = {60^0}.\) Độ dài cạnh \(b\) bằng bao nhiêu?
A. \(\sqrt {97} \) B. \(\sqrt {61} .\) C. 7 D. \(\sqrt {19} \)
Câu 18: Cho hình thoi \(ABCD\) có cạnh bằng \(a\). Góc \(\widehat {BAD} = 30^\circ \). Diện tích hình thoi \(ABCD\) là:
A. \(\frac{{{a^2}}}{4}\) B. \(\frac{{{a^2}}}{2}\) C. \(\frac{{{a^2}\sqrt 3 }}{2}\) D. \({a^2}\)
Câu 19: Cho biết \(\tan \alpha = – 5\). Giá trị của biểu thức \(E = \frac{{2\cos \alpha – 3\sin \alpha }}{{3\cos \alpha – \sin \alpha }}\) bằng bao nhiêu?
A. \(\frac{{13}}{{16}}\) B. \( – \frac{{13}}{{16}}\) C. \(\frac{{17}}{8}\) D. \( – \frac{{17}}{8}\)
Câu 20: Cho ba điểm \(A,{\rm{ }}B,{\rm{ }}C\) phân biệt. Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} .\) B. \(\overrightarrow {MP} + \overrightarrow {NM} = \overrightarrow {NP} .\) C. \(\overrightarrow {CA} + \overrightarrow {BA} = \overrightarrow {CB} .\) D. \(\overrightarrow {AA} + \overrightarrow {BB} = \overrightarrow {AB} .\)
Câu 21: Cho \(\overrightarrow a \) và \(\overrightarrow b \) là các vectơ khác \(\overrightarrow 0 \) với \(\overrightarrow a \) là vectơ đối của \(\overrightarrow b \). Khẳng định nào sau đây sai?
A. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) cùng phương. B. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) ngược hướng.
C. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) cùng độ dài. D. Hai vectơ \(\overrightarrow a ,\;\overrightarrow b \) chung điểm đầu.
Câu 22: Cho tam giác \(ABC\) cân ở \(A\), đường cao \(AH\). Khẳng định nào sau đây sai?
A. \(\overrightarrow {AB} = \overrightarrow {AC} .\) B. \(\overrightarrow {HC} = – \overrightarrow {HB} .\) C. \(\left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right|.\) D. \(\overrightarrow {BC} = 2\overrightarrow {HC} .\)
Câu 23: Cho tam giác \(ABC\) có \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \vec 0\). Xác định vị trí điểm \(M.\)
A. \(M\) thỏa mãn hình bình hành \(ACBM.\) B. \(M\) là trung điểm của đoạn thẳng \(AB.\)
C. \(M\) trùng với \(C.\) D. \(M\) là trọng tâm tam giác \(ABC.\)
Câu 24: Cho tam giác đều \(ABC\) có cạnh bằng \(a\) và chiều cao \(AH\). Mệnh đề nào sau đây là sai?
A. \(\overrightarrow {AH} .\overrightarrow {BC} = 0.\) B. \(\left( {\overrightarrow {AB} ,\overrightarrow {HA} } \right) = {150^0}.\) C. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{a^2}}}{2}.\) D. \(\overrightarrow {AC} .\overrightarrow {CB} = \frac{{{a^2}}}{2}.\)
Câu 25: Cho hình chữ nhật \(ABCD\) có \(AB = 8,{\rm{ }}AD = 5.\) Tích \(\overrightarrow {AB} .\overrightarrow {BD} .\)
A. 62 B. 64 C. 14 D. -14
II. Phần tự luận (5 điểm)
Câu 1:
a. Cho hai tập hợp \(S = \left\{ {1;2;3;4} \right\},T = \left\{ {2;4;6} \right\}\). Tìm \(S \cap T,\,\,S \cup T,\,\,S\backslash T.\)
b. Cho tập hợp \(A = \left( { – \infty ;2023} \right)\), \(B = \left[ {4 – 3m; + \infty } \right)\). Tìm \(m\) để \(\mathop C\nolimits_\mathbb{R} B \subset A\).
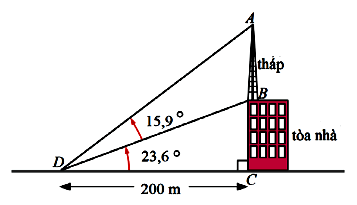
Câu 2: Một cột tháp truyền thông được xây dựng trên nóc của một tòa nhà như hình vẽ. Hãy tính chiều cao của cột tháp
Câu 3: Cho tam giác \(ABC\). Tìm điểm M thỏa mãn điều kiện:
a. \(\overrightarrow {MA} – \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
b. \(\left| {\overrightarrow {MB} – \overrightarrow {MC} } \right| = \left| {\overrightarrow {BM} – \overrightarrow {BA} } \right|\)
—– HẾT —–