Lời giải Đề bài Đề thi học kì 1 Toán 10 – Đề số 3 – Đề thi đề kiểm tra Toán lớp 10 Chân trời sáng tạo.
Câu hỏi/Đề bài:
Phần I: Trắc nghiệm (6 điểm – 30 câu).
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề?
a) Cố lên, sắp đói rồi! b) Số 15 là số nguyên tố.
c) Tổng các góc của một tam giác là \(180^\circ .\) d) \(x\) là số nguyên dương.
A. 3 B. 2 C. 4 D. 1
Câu 2: Trong các mệnh đề dưới đây mệnh đề nào đúng?
A. \(\forall {\rm{ x}} \in \mathbb{R}{\rm{, }}{{\rm{x}}^2} + 1 > 0\) B. \(\forall x \in \mathbb{R},{\rm{ }}{x^2} > x\)
C. \(\exists {\rm{ r}} \in \mathbb{Q},{\rm{ }}{{\rm{r}}^2} = 7\) D. \(\forall {\rm{ n}} \in \mathbb{N}{\rm{, n}} + 4\) chia hết cho 4.
Câu 3: Cho \(A = \left\{ {a;b;c} \right\}\) và \(B = \left\{ {a;c;d;e} \right\}\). Hãy chọn khẳng định đúng.
A. \(A \cap B = \left\{ {a;c} \right\}\) B. \(A \cap B = \left\{ {a;b;c;d;e} \right\}\) C. \(A \cap B = \left\{ b \right\}\) D. \(A \cap B = \left\{ {d;e} \right\}\)
Câu 4: Cho \(A\), \(B\) là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ bên dưới là tập hợp nào sau đây?
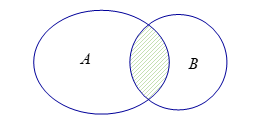
A. \(A \cup B\) B. \(B\backslash A\) C. \(A\backslash B\) D. \(A \cap B\)
Câu 5: Trong số \(50\) học sinh của lớp 10A có \(15\) bạn được xếp loại học lực giỏi, \(25\) bạn được xếp loại hạnh kiểm tốt, trong đó có \(10\) bạn vừa được xếp loại học lực giỏi vừa được xếp loại hạnh kiểm tốt. Khi đó, lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải có học lực giỏi hoặc hạnh kiểm tốt.
A. 20 B. 30 C. 35 D. 25
Câu 6: Cho \(A = \left( { – \infty ;m + 1} \right]\); \(B = \left( { – 1; + \infty } \right)\). Điều kiện để \(\left( {A \cup B} \right) = \mathbb{R}\) là
A. \(m > – 1\) B. \(m \ge – 2\) C. \(m \ge 0\) D. \(m > – 2\)
Câu 7: Trong các cặp số sau đây, cặp nào là nghiệm của bất phương trình \(2x + 3y < 1\)
A. \(\left( { – 2;1} \right)\) B. \(\left( {3; – 7} \right)\) C. \(\left( {0;1} \right)\) D. \(\left( {0;0} \right)\)
Câu 7: Hình dưới đây là hình biểu diễn của bất phương trình nào (miền nghiệm là miền màu xanh)?
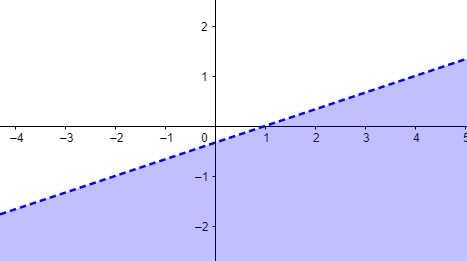
A. \(x – 3y > 1\) B. \(x – 3y < 1\) C. \(4x – 3y < 1\) D. \(4x – 3y > 1\)
Câu 8: Miền nghiệm của bất phương trình: \(3x + 2\left( {y + 3} \right) \ge 4\left( {x + 1} \right) – y + 3\) là mặt phẳng chứa điểm.
A. (3,0) B. (3,1) C. (2,1) D. (0,0)
Câu 9: Công việc nào sau đây không phụ thuộc vào các công việc của môn thống kê ?
A. Thu thập số liệu. B. Trình bày số liệu.
C. Phân tích và xử lý số liệu. D. Ra quyết định dựa trên số liệu
Câu 10: Cho mẫu số liệu thống kê \(\left\{ {6,5,5,2,9,10,8} \right\}\).Mốt của mẫu số liệu trên bằng bao nhiêu?
A. 5 B. 10 C. 2 D. 6
Câu 11: Cho dãy số liệu thống kê: 48,36,33,38,32,48,42,33,39. Khi đó số trung vị là
A. 32 B. 36 C. 38 D. 40
Câu 12: Cho dãy số liệu thống kê: \(\left\{ {8,10,12,14,16} \right\}\).Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 12 B. 14 C. 13 D. 12.5
Câu 13: Điều tra về số học sinh của 1 trường THPT có 1120 học sinh khối 10, 1075 học sinh khối 11 và 900 học sinh khối 12. Hỏi kích thước mấu là bao nhiêu?
A. 1220 B. 1075 C. 900 D. 3095
Câu 14: Chọn câu đúng trong bốn phương án trả lời đúng sau đây: độ lệch chuẩn là:
A. Bình phương của phương sai. B. Một nửa của phương sai.
C. Căn bậc hai phương sai. D. Không phải các công thức trên.
Câu 15: Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \frac{{x + 1}}{{\left( {x + 1} \right)\left( {{x^2} + 3x + 4} \right)}}.\)
A. \({\rm{D}} = \mathbb{R}\backslash \left\{ 1 \right\}.\) B. \({\rm{D}} = \left\{ { – 1} \right\}.\) C. \({\rm{D}} = \mathbb{R}\backslash \left\{ { – 1} \right\}.\) D. \({\rm{D}} = \mathbb{R}.\)
Câu 16: Điểm nào sau đây không thuộc đồ thị hàm số \(y = \frac{{\sqrt {{x^2} – 4x + 4} }}{x}.\)
A. \(A\left( {2;0} \right).\) B. \(B\left( {3;\frac{1}{3}} \right).\) C. \(C\left( {1; – 1} \right).\) D. \(D\left( { – 1; – 3} \right).\)
Câu 17: Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{\frac{{2\sqrt {x + 2} – 3}}{{x – 1}}}&{x \ge 2}\\{{x^2}{\rm{ + 1}}}&{x < 2}\end{array}} \right..\) Tính \(P = f\left( 2 \right) + f\left( { – 2} \right).\)
A. \(P = \frac{8}{3}.\) B. \(P = 4.\) C. \(P = 6.\) D. \(P = \frac{5}{3}.\)
Câu 18: Xét tính đồng biến, nghịch biến của hàm số \(f\left( x \right) = {x^2} – 4x + 5\) trên khoảng \(\left( { – \infty ;2} \right)\) và trên khoảng \(\left( {2; + \infty } \right)\). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên \(\left( { – \infty ;2} \right)\), đồng biến trên \(\left( {2; + \infty } \right)\).
B. Hàm số đồng biến trên \(\left( { – \infty ;2} \right)\), nghịch biến trên \(\left( {2; + \infty } \right)\).
C. Hàm số nghịch biến trên các khoảng \(\left( { – \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
D. Hàm số đồng biến trên các khoảng \(\left( { – \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Câu 19: Cho hàm số bậc hai \(y = {x^2} + x – 1\). Trục đối xứng của đồ thị hàm số là:
A. \(x = \frac{{ – 1}}{2}\) B. \(x = \frac{1}{2}\) C. \(y = \frac{{ – 1}}{2}\) D. \(y = \frac{{ – 1}}{2}\)
Câu 20: Tìm tất cả các giá trị thực của tham số \(m\) để hàm số \(y = \sqrt {x – m} + \sqrt {2x – m – 1} \) xác định trên \(\left( {0; + \infty } \right).\)
A. \(m \le 0.\) B. \(m \ge 1.\) C. \(m \le 1.\) D. \(m \le – 1.\)
Câu 21: Tam giác \(ABC\) có \(AB = 5,\;BC = 7,\;CA = 8\). Số đo góc \(\widehat A\) bằng:
A. \(30^\circ .\) B. \(45^\circ .\) C. \(60^\circ .\) D. \(90^\circ .\)
Câu 22: Tam giác \(ABC\) có \(AB = \sqrt 2 ,\;AC = \sqrt 3 \) và \(\widehat C = 45^\circ \). Tính độ dài cạnh \(BC\).
A. \(BC = \sqrt 5 .\) B. \(BC = \frac{{\sqrt 6 + \sqrt 2 }}{2}.\) C. \(BC = \frac{{\sqrt 6 – \sqrt 2 }}{2}.\) D. \(BC = \sqrt 6 .\)
Câu 23: Tam giác \(ABC\) có \(BC = 21{\rm{cm}},{\rm{ }}CA = 17{\rm{cm}},{\rm{ }}AB = 10{\rm{cm}}\). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\).
A. \(R = \frac{{85}}{2}{\rm{cm}}\) B. \(R = \frac{7}{4}{\rm{cm}}\) C. \(R = \frac{{85}}{8}{\rm{cm}}\) D. \(R = \frac{7}{2}{\rm{cm}}\)
Câu 24: Tam giác \(ABC\) vuông tại \(A\) có \(AB = 6\)cm, \(BC = 10\)cm. Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.
A. \(r = 1\) cm. B. \(r = \sqrt 2 \) cm C. \(r = 2\) cm. D. \(r = 3\) cm.
Câu 25: Cho hai điểm \(A\) và \(B\) phân biệt. Điều kiện để \(I\) là trung điểm \(AB\) là:
A. \(IA = IB.\) B. \(\overrightarrow {IA} = \overrightarrow {IB} .\) C. \(\overrightarrow {IA} = – \overrightarrow {IB} .\) D. \(\overrightarrow {AI} = \overrightarrow {BI} .\)
Câu 26: Cho \(\overrightarrow {AB} = – \overrightarrow {CD} \). Khẳng định nào sau đây đúng?
A. \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng. B. \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng độ dài.
C. \(ABCD\) là hình bình hành. D. \(\overrightarrow {AB} + \overrightarrow {DC} = \overrightarrow 0 .\)
Câu 27: Cho hình bình hành \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Hỏi vectơ \(\left( {\overrightarrow {AO} – \overrightarrow {DO} } \right)\) bằng vectơ nào trong các vectơ sau?
A. \(\overrightarrow {BA} .\) B. \(\overrightarrow {BC} .\) C. \(\overrightarrow {DC} .\) D. \(\overrightarrow {AC} .\)
Câu 28: Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(\overrightarrow {AB} .\overrightarrow {AC} .\)
A. \(\overrightarrow {AB} .\overrightarrow {AC} = {a^2}.\) B. \(\overrightarrow {AB} .\overrightarrow {AC} = {a^2}\sqrt 2 .\) C. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{\sqrt 2 }}{2}{a^2}.\) D. \(\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}{a^2}.\)
Câu 29: Cho hình thoi \(ABCD\) có \(AC = 8\) và \(BD = 6.\) Tính \(\overrightarrow {AB} .\overrightarrow {AC} .\)
A. \(\overrightarrow {AB} .\overrightarrow {AC} = 24.\) B. \(\overrightarrow {AB} .\overrightarrow {AC} = 26.\) C. \(\overrightarrow {AB} .\overrightarrow {AC} = 28.\) D. \(\overrightarrow {AB} .\overrightarrow {AC} = 32.\)
Câu 30: Cho hình bình hành \(ABCD\) có \(AB = 8\,\,{\rm{cm, }}AD = 12\,\,{\rm{cm}}\), góc \(\widehat {ABC}\) nhọn và diện tích bằng \(54\,\,{\rm{c}}{{\rm{m}}^2}.\) Tính \(\cos \left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right).\)
A. \(\frac{{2\sqrt 7 }}{{16}}\) B. \( – \frac{{2\sqrt 7 }}{{16}}\) C. \(\frac{{5\sqrt 7 }}{{16}}\) D. \( – \frac{{5\sqrt 7 }}{{16}}\)
Phần II. Tự luận (4 điểm):
Câu 1:
a. Cho hai tập hợp \(A = \left[ { – 2;3} \right]\) và \(B = \left( {1; + \infty } \right)\). Tìm \(A \cap B\).
b. Cho \(m\) là một tham số thực và hai tập hợp \(A = \left[ {1 – 2m;\,m + 3} \right]\), \(B = \left\{ {x \in \mathbb{R}|\,x \ge 8 – 5m} \right\}\). Tìm các giá trị \(m\) để \(A \cap B = \emptyset \).
Câu 2: Cho hàm số \(y = {x^2} – 2\left( {m + 1} \right)x + 3m – 3\)có đồ thị (P). Biết hàm số đi qua M (3, 0)
a. Xác định hàm số
b. Vẽ bảng biến thiên, vẽ đồ thị (P).
Câu 3: Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng \(CD = 60{\rm{m}}\), giả sử chiều cao của giác kế là \(OC = 1{\rm{m}}\). Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh \(A\) của tháp. Đọc trên giác kế số đo của góc \(\widehat {AOB} = {60^0}\). Tính chiều cao của tháp, làm tròn kết quả đến hàng phần trăm.
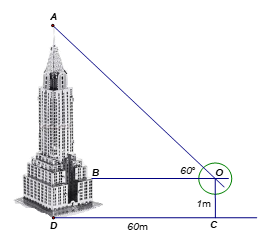
Câu 4: Tìm tập các hợp điểm \(M\) thỏa mãn \(\overrightarrow {MB} \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\) với \(A,{\rm{ }}B,{\rm{ }}C\) là ba đỉnh của tam giác.
—–HẾT—-