Trang chủ Lớp 10 Toán lớp 10 Đề thi đề kiểm tra Toán lớp 10 - Cánh diều Đề kiểm tra học kì 2 Toán 10 – Đề số 2...

Đề kiểm tra học kì 2 Toán 10 – Đề số 2 – Cánh diều: PHẦN TRẮC NGHIỆM (7, 0 điểm) Từ thành phố A tới thành phố B có 4 con đường, từ thành phố B tới thành phố C có 6 con đường

Gợi ý giải Đề kiểm tra học kì 2 Toán 10 – Đề số 2 – Cánh diều – Đề thi học kì 2 – Đề thi đề kiểm tra Toán lớp 10 Cánh diều. I. PHẦN TRẮC NGHIỆM ( 35 câu – 7,0 điểm )….

Đề thi:

PHẦN TRẮC NGHIỆM (7,0 điểm)

Câu 1. Từ thành phố \(A\) tới thành phố \(B\) có \(4\) con đường, từ thành phố \(B\) tới thành phố \(C\) có \(6\) con đường. Hỏi có bao nhiêu cách đi từ \(A\) tới \(C\) qua \(B\)?

A. \(24\). B. \(7\). C. \(6\). D. \(12\).

Câu 2. Tính số chỉnh hợp chập \(3\) của \(5\) phần tử.

A. \(10\). B. \(720\). C. \(60\). D. \(6\).

Câu 3. Một tổ có \(7\) học sịnh nam và \(11\) học sinh nữ. Hỏi có bao nhiêu cách chọn \(7\) học sinh đi lao động, trong đó có đúng \(3\) học sinh nam?

A. \(C_7^3 + C_{11}^4\). B. \(C_7^3C_{15}^4\). C. \(A_7^3A_{11}^4\). D. \(C_7^3C_{11}^4\).

Câu 4. Số hạng tổng quát trong khai triển của \({\left( {3 – 5x} \right)^{16}}\) là:

A. \({\left( { – 3} \right)^k}C_{16}^k5{x^k}\).

B. \({\left( { – 3} \right)^k}C_{16}^k{5^k}{x^k}\).

C. \({\left( { – 3} \right)^{16 – k}}C_{16}^k{5^k}{x^k}\).

D. \(C_{16}^k{5^k}{x^{16 – k}}\).

Câu 5. Cho khai triển \({\left( {1 – 2x} \right)^{30}} = {a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_{30}}{x^{30}}\). Giá trị của \({a_0} + {a_1} + {a_2} + \cdots + {a_{30}}\) bằng:

A. \(1\). B. \({3^{30}}\). C. \(0\). D. \( – 1\).

Câu 6. Tìm số hạng không chứa \(x\) trong khai triển nhị thức Newton \({\left( {x – \frac{4}{{{x^2}}}} \right)^{27}}\), \(\left( {x \ne 0,\,\,n \in {\mathbb{N}^*}} \right)\).

A. \({4^9}C_{27}^9\).

B. \({4^{18}}C_{27}^{18}\).

C. \( – {4^{18}}C_{27}^{18}\).

D. \( – {4^9}C_{27}^9\).

Câu 7. Từ các chữ số \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) có thể lập được bao nhiêu số gồm \(4\) chữ số khác nhau và không chia hết cho \(5\)?

A. \(4088\). B. \(4032\). C. \(3584\). D. \(952\).

Câu 8. Tính số cách xếp \(9\) quyển sách Toán, \(8\) quyển sách Lý và \(7\) quyển sách Hóa lên một giá sách theo từng môn.

A. \(9!.8!.7!\). B. \(9! + 8! + 7!\). C. \(9!.8!.7!.3!\). D. \(9.8.7\).

Câu 9. Cho một đa giác đều có \(24\) đỉnh nội tiếp trong một đường tròn tâm \(O\). Gọi \(X\) là tập các tam giác có các đỉnh là các đỉnh của đa giá trên. Tính xác suất để chọn được một tam giác từ tập \(X\) là tam giác cân nhưng không phải là tam giác đều.

A. \(\frac{{32}}{{253}}\).

B. \(\frac{3}{{23}}\).

C. \(\frac{{221}}{{253}}\).

D. \(\frac{1}{{253}}\).

Câu 10. Kết quả đo chiều dài của một cây cầu được ghi là \(154m \pm 0,4m\). Tìm sai số tương đối của phép đo chiều dài cây cầu.

A. \({\delta _a} < 0,25974\% \).

B. \({\delta _a} < 1,25974\% \).

C. \({\delta _a} = 0,25974\% \).

D. \({\delta _a} > 0,25974\% \).

Câu 11. Giá của một số loại giày (đơn vị nghìn đồng) như sau:

Mốt của mẫu số liệu trên là

A. \(400\). B. \(500\). C. \(300\). D. \(600\).

Câu 12. Cho mẫu số liệu gồm \(20\) số dương không hoàn toàn giống nhau. Khoảng tứ phân vị sẽ thay đổi như thế nào nếu nhân mỗi giá trị của mẫu số liệu với \(2\)

A. Giảm \(2\) lần. B. Tăng \(2\) lần. C. Giữ nguyên. D. Tăng \(4\) lần.

Câu 13. Từ mẫu số liệu về thuế thuốc lá của \(69\) thành phố tại một quốc gia, người ta tính được: Giá trị nhỏ nhất bằng \(2,5\); \({Q_1} = 36\); \({Q_2} = 60\); \({Q_3} = 100\); giá trị lớn nhất bằng \(205\). Hỏi tỷ lệ thành phố có thuế thuốc lá lớn hơn \(36\) là bao nhiêu?

A. \(\frac{{35}}{{69}}\). B. \(\frac{{34}}{{69}}\). C. \(\frac{{17}}{{69}}\). D. \(\frac{{52}}{{69}}\).

Câu 14. Nhiệt độ của thành phố Hà Nội đo trong \(30\) ngày có nhiệt độ lớn nhất là \(35^\circ {\rm{C}}\), nhỏ nhất là \(27^\circ {\rm{C}}\); \({Q_1} = 30\); \({Q_3} = 33\). Hỏi trong \(30\) ngày có bao nhiêu ngày nhiệt độ nhỏ hơn \(33^\circ {\rm{C}}\)?

A. \(8\). B. \(22\). C. \(7\). D. \(14\).

Câu 15. Thời gian chạy của một học sinh chạy \(100\,m\) được ghi lại trong \(6\) lần là

Tìm số trung bình của mẫu số liệu trên

A. \(15,22\). B. \(10,87\). C. \(12,68\). D. \(13,84\).

Câu 16. Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm lẻ xuất hiện là

A. \(1\). B. \(\frac{1}{2}\). C. \(\frac{1}{3}\). D. \(\frac{2}{3}\).

Câu 17. Gieo hai con súc sắc cân đối, đồng chất. Xác suất để tổng số chấm xuất hiện trên hai mặt của hai con súc sắc bằng \(6\) là

A. \(\frac{{31}}{{36}}\). B. \(\frac{1}{6}\). C. \(\frac{5}{{36}}\). D. \(\frac{5}{6}\).

Câu 18. Gieo một con súc sắc cân đối và đồng chất. Tính xác suất để xuất hiện mặt có số chấm không chia hết cho \(3\).

A. \(1\). B. \(\frac{2}{3}\). C. \(3\). D. \(\frac{1}{3}\).

Câu 19. Trong trò chơi “Chiếc nón kỳ diệu” chiếc kim của bánh xe có thể dừng lại ở một trong \(9\) vị trí với khả năng như nhau. Tính xác suất để trong ba lần quay, chiếc kim của bánh xe đó lần lượt dừng lại ở ba vị trí khác nhau.

A. \(\frac{{28}}{{243}}\). B. \(\frac{{56}}{{81}}\). C. \(\frac{8}{{243}}\). D. \(\frac{8}{{81}}\).

Câu 20. Lấy ngẫu nhiên hai viên bi từ một thùng gồm \(7\) bi xanh, \(8\) bi đỏ và \(9\) bi vàng. Tính xác suất để lấy được hai viên bi khác màu?

A. \(76,45\% \). B. \(23,54\% \). C. \(30,8\% \). D. \(69,2\% \).

Câu 21. Lớp \(11B\) có \(30\) đoàn viên trong đó có \(19\) nam. Chọn ngẫu nhiên \(3\) đoàn viên trong lớp để tham dự hội trại ngày \(26\) tháng \(3\). Tính xác suất để \(3\) đoàn viên được chọn có \(2\) nữ và \(1\) nam.

A. \(\frac{{1881}}{{4060}}\).

B. \(\frac{{603}}{{812}}\).

C. \(\frac{{209}}{{812}}\).

D. \(\frac{{2179}}{{4060}}\).

Câu 22. Một cái hộp chứa \(9\) viên bi đỏ và \(8\) viên bi xanh. Lấy lần lượt \(2\) viên bi từ cái hộp đó. Tính xác suất để viên bi được lấy lần thứ \(2\) là bi xanh.

A. \(\frac{8}{{17}}\).

B. \(\frac{{25}}{{68}}\).

C. \(\frac{{25}}{{34}}\).

D. \(\frac{9}{{17}}\).

Câu 23. Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( {2\,;\,5} \right)\); \(B\left( {3\,;\,7} \right)\). Tìm tọa độ của véctơ \(\overrightarrow {AB} \).

A. \(\left( { – 1\,;\, – 2} \right)\).

B. \(\left( {1\,;\,2} \right)\).

C. \(\left( {5\,;\,12} \right)\).

D. \(\left( {2\,;\,1} \right)\).

Câu 24. Trong mặt phẳng \(Oxy\), cho \(\vec a = \left( {2\,;\,6} \right)\); \(\vec b = \left( { – 1\,;\,3} \right)\). Tọa độ vectơ \(4\overrightarrow a – 3\overrightarrow b \) là:

A. \(\left( { – 11\,;\,15} \right)\).

B. \(\left( {15\,;\, – 11} \right)\).

C. \(\left( {15\,;\,11} \right)\).

D. \(\left( {11\,;\,15} \right)\).

Câu 25. Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( {5\,;\,4} \right)\);\(B\left( { – 2\,;\,7} \right)\). Xác định tọa độ điểm \(E\) trên đoạn \(AB\) sao cho \(AE = 3EB\).

A. \(E\left( { – \frac{1}{4}\,;\,\frac{{25}}{4}} \right)\).

B. \(E\left( { – \frac{1}{4}\,;\, – \frac{{25}}{4}} \right)\).

C. \(E\left( {\frac{1}{4}\,;\,\frac{{25}}{4}} \right)\).

D. \(E\left( {\frac{1}{4}\,;\, – \frac{{25}}{4}} \right)\).

Câu 26. Cho đường thẳng \(d:3x + 5y – 7 = 0\). Véc tơ nào sau đây là véctơ chỉ phương của \(d\)?

A. \(\overrightarrow u = \left( {3\,;\, – 5} \right)\).

B. \(\overrightarrow u = \left( {5\,;\,3} \right)\).

C. \(\overrightarrow u = \left( {5\,;\, – 3} \right)\).

D. \(\overrightarrow u = \left( {3\,;\,5} \right)\).

Câu 27. Trong hệ tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {3\,;\,6} \right)\); \(B\left( { – 1\,;\,5} \right)\); \(C\left( {3\,;\,3} \right)\). Phương trình đường trung tuyến kẻ từ đỉnh \(A\) của tam giác \(ABC\) là:

A. \(x – y + 3 = 0\). B. \(x + y – 9 = 0\). C. \(x + 2y – 15 = 0\). D. \(x – 2y = 0\).

Câu 28. Tìm các giá trị thực của tham số \(m\) để đường thẳng \(y = \left( {{m^2} – 6} \right)x + 2m + 5\) song song với đường thẳng \(y = 3x – 1\).

A. \(m = \pm 3\). B. \(m = \pm 2\). C. \(m = – 3\). D. \(m = 3\).

Câu 29. Trong mặt phẳng tọa độ \({\rm{Ox}}y\), gọi \(d\) là đường thẳng đi qua \(M\left( {3\,;\,4} \right)\) và cách điểm \(A\left( {2\,;\,5} \right)\) một khoảng bằng \(\frac{{3\sqrt 5 }}{5}\). Biết rằng phương trình đường thẳng \(d\) có dạng \(x + by + c = 0\) với \(b\); \(c\) là hai số nguyên. Tính \(b + c\).

A. \(7\). B. \( – 3\). C. \(3\). D. \(7\).

Câu 30. Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} + {y^2} + 2\left( {m – 3} \right)x + 6my + 9m + 19 = 0\) là phương trình đường tròn.

A. \( – \frac{1}{2} < m < 2\).

B. \(m \frac{1}{2}\).

C. \(m 2\).

D. \(m 2\).

Câu 31. Trong mặt phẳng \(Oxy\), đường tròn \(\left( C \right):{x^2} + {y^2} + 6x + 2y – 26 = 0\) có tâm là

A. \(I\left( { – 3\,;\, – 1} \right)\).

B. \(I\left( {3\,;\,1} \right)\).

C. \(I\left( {2\,;\,6} \right)\).

D. \(I\left( { – 2\,;\, – 6} \right)\).

Câu 32. Trên mặt phẳng toạ độ \(Oxy\), cho các điểm \(A\left( {8\,;\,0} \right)\) và \(B\left( {0\,;\,6} \right)\). Đường tròn nội tiếp tam giác \(OAB\) có phương trình

A. \({\left( {x – 4} \right)^2} + {\left( {y – 4} \right)^2} = 16\).

B. \({\left( {x – 3} \right)^2} + {\left( {y – 3} \right)^2} = 9\).

C. \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} = 1\).

D. \({\left( {x – 2} \right)^2} + {\left( {y – 2} \right)^2} = 4\).

Câu 33. Cặp điểm nào là các tiêu điểm của elip \(\left( E \right)\): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\)?

A. \({F_1} = \left( {0\,;\,2} \right)\); \({F_2} = \left( {0\,;\, – 2} \right)\).

B. \({F_1} = \left( {2\,;\,0} \right)\); \({F_2} = \left( { – 2\,;\,0} \right)\).

C. \({F_1} = \left( {3\,;\,0} \right)\); \({F_2} = \left( { – 3\,;\,0} \right)\).

D. \({F_1} = \left( {0\,;\,3} \right)\); \({F_2} = \left( {0\,;\, – 3} \right)\).

Câu 34. Ông Hoàng có một mảnh vườn hình elip có chiều dài trục lớn và trục nhỏ lần lượt là \(80\,m\) và \(40\,m\). Ông chia thành hai nửa bằng một đường tròn tiếp xúc trong với elip để làm mục đích sử dụng khác nhau. Nửa bên trong đường tròn ông trồng cây lâu năm, nửa bên ngoài đường tròn ông trồng hoa màu. Tính tỷ số diện tích \(T\) giữa phần trồng cây lâu năm so với diện tích trồng hoa màu. Biết diện tích elip được tính theo công thức \(S = \pi ab\) trong đó \(a\); \(b\) lần lượt là độ dài nửa trục lớn và nửa trục bé của elip, biết độ rộng của đường elip không đáng kể.

A. \(T = \frac{2}{3}\). B. \(T = 1\). C. \(T = \frac{1}{3}\). D. \(T = \frac{3}{2}\).

Câu 35. Cho elip . Tìm toạ độ điểm \(M \in \left( E \right)\) sao cho M nhìn \({F_1}{F_2}\) dưới một góc vuông:

A. \(M\left( {\sqrt 6 \,;\,\frac{{\sqrt {30} }}{2}} \right)\); \(M\left( { – \sqrt 6 \,;\,\frac{{\sqrt {30} }}{2}} \right)\); \(M\left( {\sqrt 6 \,;\, – \frac{{\sqrt {30} }}{2}} \right)\); \(M\left( { – \sqrt 6 \,;\, – \frac{{\sqrt {30} }}{2}} \right)\).

B. \(M\left( {\sqrt 3 \,;\,\frac{{\sqrt {33} }}{2}} \right)\); \(M\left( { – \sqrt 3 \,;\,\frac{{\sqrt {33} }}{2}} \right)\); \(M\left( {\sqrt 3 \,;\, – \frac{{\sqrt {33} }}{2}} \right)\); \(M\left( { – \sqrt 3 \,;\, – \frac{{\sqrt {33} }}{2}} \right)\).

C. \(M\left( {2\sqrt 3 \,;\,\sqrt 6 } \right)\); \(M\left( { – 2\sqrt 3 \,;\,\sqrt 6 } \right)\); \(M\left( {2\sqrt 3 \,;\, – \sqrt 6 } \right)\); \(M\left( { – 2\sqrt 3 \,;\, – \sqrt 6 } \right)\).

D. \(M\left( {2\sqrt 6 \,;\,\sqrt 3 } \right)\); \(M\left( { – 2\sqrt 6 \,;\,\sqrt 3 } \right)\); \(M\left( {2\sqrt 6 \,;\, – \sqrt 3 } \right)\); \(M\left( { – 2\sqrt 6 \,;\, – \sqrt 3 } \right)\).

PHẦN TỰ LUẬN (3,0 điểm)

Bài 1. (1,0 điểm) Từ \(2\) chữ số \(1\) và \(9\) lập được bao nhiêu số tự nhiên có \(9\) chữ số sao cho không có \(2\) chữ số \(1\) đứng cạnh nhau?

Bài 2. (0,5 điểm) Cho đa giác đều \(2023\) đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn \(120^\circ \)?

Bài 3. (1,0 điểm) Trong mặt phẳng tọa độ \(Oxy\), cho ba điểm \(A\left( {2\,;\,5} \right)\); \(B\left( {4\,;\,1} \right)\); \(C\left( { – 3\,;\,3} \right)\). Tìm tọa độ điểm \(M\) trên đường thẳng \(d:2x – 3y + 20 = 0\) sao cho \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất.

Bài 4. (0,5 điểm) Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(A\left( {5\,;\,2} \right)\); \(B\left( {1\,;\,9} \right)\) và điểm \(M\) thay đổi thuộc đường tròn \(\left( C \right):{x^2} + {y^2} – 2x – 4y + 1 = 0\). Tìm giá trị nhỏ nhất của biểu thức \(P = MA + 2MB\).

Đáp án Đề thi:

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHYÊN MÔN GiaiBaitapsgk.COM

I. PHẦN TRẮC NGHIỆM (35 câu – 7,0 điểm).

A. \(24\). B. \(7\). C. \(6\). D. \(12\).

Phương pháp

Áp dụng quy tắc nhân

Lời giải

Chọn A

Từ \(A\) đến \(B\) có \(4\) cách chọn đường đi, từ \(B\) đến \(C\) có \(6\) cách chọn đường đi.

Vậy số cách chọn đường đi từ \(A\) đến \(C\) phải đi qua \(B\) là : \(4.6 = 24\) cách.

Câu 2. Tính số chỉnh hợp chập \(3\) của \(5\) phần tử.

A. \(10\). B. \(720\). C. \(60\). D. \(6\).

Phương pháp

Áp dụng công thức chỉnh hợp

Lời giải

Chọn C

Ta có: \(A_5^3 = \frac{{5!}}{{2!}} = 60\).

Câu 3. Một tổ có \(7\) học sịnh nam và \(11\) học sinh nữ. Hỏi có bao nhiêu cách chọn \(7\) học sinh đi lao động, trong đó có đúng \(3\) học sinh nam?

A. \(C_7^3 + C_{11}^4\).

B. \(C_7^3C_{15}^4\).

C. \(A_7^3A_{11}^4\).

D. \(C_7^3C_{11}^4\).

Phương pháp

Số tổ hợp chập k của n phần tử là \(C_n^k = \frac{{n!}}{{\left( {n – k} \right)!k!}}\)

Lời giải

Chọn D

Chọn \(3\) học sinh nam, có \(C_7^3\) cách.

Chọn \(4\) học sinh nữ, có \(C_{11}^4\) cách.

Vậy có \(C_7^3C_{11}^4\) cách chọn thỏa yêu cầu bài toán.

Câu 4. Số hạng tổng quát trong khai triển của \({\left( {3 – 5x} \right)^{16}}\) là:

A. \({\left( { – 3} \right)^k}C_{16}^k5{x^k}\).

B. \({\left( { – 3} \right)^k}C_{16}^k{5^k}{x^k}\).

C. \({\left( { – 3} \right)^{16 – k}}C_{16}^k{5^k}{x^k}\).

D. \(C_{16}^k{5^k}{x^{16 – k}}\).

Phương pháp

Số hạng tổng quát trong khai triển \({\left( {a + b} \right)^n}\) có dạng: \(C_n^k{a^{n – k}}{b^k}\).

Lời giải

Chọn C

Số hạng tổng quát trong khai triển \({\left( {a + b} \right)^n}\) có dạng: \(C_n^k{a^{n – k}}{b^k}\).

Do đó số hạng tổng quát trong khai triển của \({\left( {3 – 5x} \right)^{16}} = {\left( { – 3 + 5x} \right)^{16}}\) là: \(C_{16}^k{\left( { – 3} \right)^{16 – k}}{\left( {5x} \right)^k} = {\left( { – 3} \right)^{16 – k}}C_{16}^k{5^k}{x^k}\).

Câu 5. Cho khai triển \({\left( {1 – 2x} \right)^{30}} = {a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_{30}}{x^{30}}\). Giá trị của \({a_0} + {a_1} + {a_2} + \cdots + {a_{30}}\) bằng:

A. \(1\). B. \({3^{30}}\). C. \(0\). D. \( – 1\).

Lời giải

Chọn A

\({\left( {1 – 2x} \right)^{30}} = {a_0} + {a_1}x + {a_2}{x^2} + \cdots + {a_{30}}{x^{30}}\) \(\left( 1 \right)\).

Thay \(x = 1\) vào \(\left( 1 \right)\) ta có: \(\)\({a_0} + {a_1} + {a_2} + \cdots + {a_{30}} = {\left( { – 1} \right)^{30}} = 1\).

Câu 6. Tìm số hạng không chứa \(x\) trong khai triển nhị thức Newton \({\left( {x – \frac{4}{{{x^2}}}} \right)^{27}}\), \(\left( {x \ne 0,\,\,n \in {\mathbb{N}^*}} \right)\).

A. \({4^9}C_{27}^9\).

B. \({4^{18}}C_{27}^{18}\).

C. \( – {4^{18}}C_{27}^{18}\).

D. \( – {4^9}C_{27}^9\).

Phương pháp

Số hạng tổng quát trong khai triển \({\left( {a + b} \right)^n}\) có dạng: \(C_n^k{a^{n – k}}{b^k}\).

Lời giải

Chọn D

Ta có \(C_n^k{a^{n – k}}{b^k} = C_{27}^k{x^{27 – k}}.{\left( { – \frac{4}{{{x^2}}}} \right)^k} = {\left( { – 4} \right)^k}C_{27}^k{x^{27 – 3k}}\).

Theo yêu cầu bài toán\( \Leftrightarrow 27 – 3k = 0 \Leftrightarrow k = 9\). Vậy hệ số cần tìm là \( – {4^9}C_{27}^9\).

A. \(4088\). B. \(4032\). C. \(3584\). D. \(952\).

Phương pháp

Áp dụgn các quy tắc đếm

Lời giải

Chọn C

Gọi số cần tìm dạng: \(\overline {abcd} \), \(\left( {a \ne 0} \right)\).

Số các số tự nhiên có \(4\) chữ số khác nhau là: \(9.A_9^3 = 4536\) số.

Số các số tự nhiên có \(4\) chữ số khác nhau chia hết cho \(5\) là: \(A_9^3 + 8.A_8^2 = 952\) số.

Vậy số các số tự nhiên có \(4\) chữ số khác nhau không chia hết cho \(5\) là: \(4536 – 952 = 3584\) số.

Câu 8. Tính số cách xếp \(9\) quyển sách Toán, \(8\) quyển sách Lý và \(7\) quyển sách Hóa lên một giá sách theo từng môn.

A. \(9!.8!.7!\). B. \(9! + 8! + 7!\). C. \(9!.8!.7!.3!\). D. \(9.8.7\).

Phương pháp

Áp dụgn các quy tắc đếm

Lời giải

Chọn C

Các bước thực hiện:

* Bước 1: Chọn vị trí cho từng môn học\( \Rightarrow \) Có \(3!\) cách.

* Bước 2: Xếp sách Toán vào\( \Rightarrow \) Có \(9!\) cách.

* Bước 3: Xếp sách Lý vào\( \Rightarrow \) Có \(8!\) cách.

* Bước 4: Xếp sách Hóa vào\( \Rightarrow \) Có \(7!\) cách.

Áp dụng quy tắc nhân ta có tổng số cách xếp là: \(9!.8!.7!.3!\) cách.

A. \(\frac{{32}}{{253}}\).

B. \(\frac{3}{{23}}\).

C. \(\frac{{221}}{{253}}\).

D. \(\frac{1}{{253}}\).

Phương pháp

Áp dụng công thức tính xác suất

Lời giải

Chọn A

Số các tam giác bất kỳ là \(n\left( \Omega \right) = C_{24}^3\).

Số các tam giác đều là \(\frac{{24}}{3} = 8\).

Có \(24\) cách chọn một đỉnh của đa giác, mỗi đỉnh có \(11\) các chọn \(2\) đỉnh còn lại để được một tam giác cân.

Số các tam giác cân là: \(24.11 = 264\).

Số các tam giác cân không đều là: \(264 – 8 = 256 \Rightarrow n\left( A \right) = 256\).

\( \Rightarrow P\left( A \right) = \frac{{256}}{{C_{24}^3}} = \frac{{32}}{{253}}\).

Câu 10. Kết quả đo chiều dài của một cây cầu được ghi là \(154m \pm 0,4m\). Tìm sai số tương đối của phép đo chiều dài cây cầu.

A. \({\delta _a} < 0,25974\% \).

B. \({\delta _a} < 1,25974\% \).

C. \({\delta _a} = 0,25974\% \).

D. \({\delta _a} > 0,25974\% \).

Phương pháp

Ta nói a là số gần đúng của số đúng \(\overline a \) với độ chính xác d nếu \({\Delta _a} = \left| {\overline a – a} \right| \le d\) và quy ước viết gọn là \(\overline a = a \pm d\)

Tỉ số \({\delta _a} = \frac{{{\Delta _a}}}{{\left| a \right|}}\) được gọi là sai số tương đối của số gần đúng a.

Lời giải

Chọn A

Sai số tương đối \({\delta _a} \le \frac{{0,4}}{{154}} \approx 0,0025974 \approx 0,25974\% \).

Câu 11. Giá của một số loại giày (đơn vị nghìn đồng) như sau:

Mốt của mẫu số liệu trên là

A. \(400\). B. \(500\). C. \(300\). D. \(600\).

Phương pháp

Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tần số và kí hiệu là \({M_0}\).

Lời giải

Chọn A

Số \(400\) xuất hiện nhiều nhất trên mẫu số liệu trên nên mốt là \(400\).

Câu 12. Cho mẫu số liệu gồm \(20\) số dương không hoàn toàn giống nhau. Khoảng tứ phân vị sẽ thay đổi như thế nào nếu nhân mỗi giá trị của mẫu số liệu với \(2\).

A. Giảm \(2\) lần. B. Tăng \(2\) lần. C. Giữ nguyên. D. Tăng \(4\) lần.

Phương pháp

Giả sử \({Q_1},{Q_2},{Q_3}\) là tứ phân vị của mẫu số liệu. Ta gọi hiệu \({\Delta _Q} = {Q_3} – {Q_1}\) là khoảng tứ phân vị của mẫu số liệu đó.

Lời giải

Chọn B

Nhân mỗi giá trị của mẫu số liệu với \(2\) thì khoảng tứ phân vị tăng gấp \(2\) lần.

A. \(\frac{{35}}{{69}}\).

B. \(\frac{{34}}{{69}}\).

C. \(\frac{{17}}{{69}}\).

D. \(\frac{{52}}{{69}}\).

Phương pháp

Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm.

Tứ phân vị của mẫu số liệu trên là bộ ba giá trị : Tứ phân vị thứ nhất, Tứ phân vị thứ hai và Tứ phân vị thứ ba; ba giá trị này chia mẫu số liệu thành bốn phần có số lượng phần tử bằng nhau.

– Tứ phân vị thứ hai \({Q_2}\) bằng trung vị.

– Nết n chẵn thì tứ phân vị thứ nhất \({Q_2}\) bằng trung vị của nửa dãy phía dưới, và tứ phân vị thứ ba \({Q_3}\) bằng trung vị của nửa dãy phía trên.

– Nếu n là số lẻ thì tứ phân vị thứ nhất \({Q_2}\) bằng trung vị của nửa dãy phía dưới (không bào gồm \({Q_2}\)) và tứ phân vị thứ ba \({Q_2}\) bằng trung vị của nửa dãy phía trên ( không bao gồm \({Q_2}\))

Lời giải

Chọn D

Từ mẫu số liệu về thuế thuốc lá của \(69\) thành phố tại một quốc gia, người ta tính được \({Q_1} = 36\) nên có \(52\) thành phố có thuế thuốc lá lớn hơn \(36\).

Vì vậy, tỷ lệ thành phố có thuế thuốc lá lớn hơn 36 là: \(\frac{{52}}{{69}}\).

A. \(8\). B. \(22\). C. \(7\). D. \(14\).

Phương pháp

Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm.

– Tứ phân vị thứ hai \({Q_2}\) bằng trung vị.

– Nết n chẵn thì tứ phân vị thứ nhất \({Q_2}\) bằng trung vị của nửa dãy phía dưới, và tứ phân vị thứ ba \({Q_3}\) bằng trung vị của nửa dãy phía trên.

Lời giải

Chọn B

Vì \({Q_3} = 33\) nên có \(22\) ngày nhiệt độ nhỏ hơn \(33^\circ {\rm{C}}\).

Câu 15. Thời gian chạy của một học sinh chạy \(100\,m\) được ghi lại trong \(6\) lần là

Tìm số trung bình của mẫu số liệu trên

A. \(15,22\). B. \(10,87\). C. \(12,68\). D. \(13,84\).

Phương pháp

Số trung bình cộng \(\overline x \) của mẫu số liệu \({x_1},{x_2},…,{x_n}\) là:

\(\overline x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}.\)

Lời giải

Chọn C

Số trung bình của mẫu số liệu trên là \(\overline x = \frac{{13,5 + 12,1 + 12,8 + 13,2 + 12,1 + 12,4}}{6} = \frac{{761}}{{60}} \approx 12,68\).

Câu 16. Gieo một con súc sắc cân đối và đồng chất, xác suất để mặt có số chấm lẻ xuất hiện là

A. \(1\). B. \(\frac{1}{2}\). C. \(\frac{1}{3}\). D. \(\frac{2}{3}\).

Phương pháp

Áp dụng công thức tính xác suất

Lời giải

Chọn B

Ta có: Không gian mẫu \(\Omega = \left\{ {1,2,3,4,5,6} \right\}\).

Suy ra \(n\left( \Omega \right) = 6\).

Gọi biến cố \(A\): “Con súc sắc có số chấm lẻ xuất hiện” hay \(A = \left\{ {1;3;5} \right\}\) suy ra \(n\left( A \right) = 3\).

Từ đó suy ra \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{3}{6} = \frac{1}{2}\).

Vậy xác suất để mặt có số chấm lẻ xuất hiện là \(\frac{1}{2}\).

Câu 17. Gieo hai con súc sắc cân đối, đồng chất. Xác suất để tổng số chấm xuất hiện trên hai mặt của hai con súc sắc bằng \(6\) là

A. \(\frac{{31}}{{36}}\).

B. \(\frac{1}{6}\).

C. \(\frac{5}{{36}}\).

D. \(\frac{5}{6}\).

Phương pháp

Áp dụng công thức tính xác suất

Lời giải

Chọn C

Số phần tử của không gian mẫu là \(n\left( \Omega \right) = 6 \times 6 = 36\).

Gọi \(A\) là biến cố “Tổng số chấm xuất hiện trên hai mặt của hai con súc sắc bằng \(6\)”.

Ta có \(A = \left\{ {\left( {1;5} \right),\left( {2;4} \right),\left( {3;3} \right),\left( {4;2} \right),\left( {5;1} \right)} \right\}\)\( \Rightarrow \)\(n\left( A \right) = 5\).

Vậy \(P\left( A \right) = \frac{5}{{36}}\).

Câu 18. Gieo một con súc sắc cân đối và đồng chất. Tính xác suất để xuất hiện mặt có số chấm không chia hết cho \(3\).

A. \(1\).

B. \(\frac{2}{3}\).

C. \(3\).

D. \(\frac{1}{3}\).

Phương pháp

Áp dụng công thức tính xác suất

Lời giải

Chọn B

Ta có \(n\left( \Omega \right) = 6\).

Mà \(A = \left\{ {1\,;\,2\,;\,4\,;\,5} \right\}\)\( \Rightarrow \)\(n\left( A \right) = 4\).

Vậy \(P\left( A \right) = \frac{4}{6} = \frac{2}{3}\).

A. \(\frac{{28}}{{243}}\).

B. \(\frac{{56}}{{81}}\).

C. \(\frac{8}{{243}}\).

D. \(\frac{8}{{81}}\).

Phương pháp

Áp dụng công thức tính xác suất

Lời giải

Chọn B

Số phần tử của không gian mẫu là \(n\left( \Omega \right) = C_9^1C_9^1C_9^1 = {9^3}\).

Gọi \(A\) là biến cố “Trong ba lần quay, chiếc kim của bánh xe dừng lại ở ba vị trí khác nhau”.

Số kết quả thuận lợi cho biến cố \(A\) là \(n\left( A \right) = C_9^1C_8^1C_7^1\).

Vậy xác suất của biến cố \(A\) là \(\mathbb{P}\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_9^1C_8^1C_7^1}}{{{9^3}}} = \frac{{56}}{{81}}\).

Câu 20. Lấy ngẫu nhiên hai viên bi từ một thùng gồm \(7\) bi xanh, \(8\) bi đỏ và \(9\) bi vàng. Tính xác suất để lấy được hai viên bi khác màu?

A. \(76,45\% \). B. \(23,54\% \). C. \(30,8\% \). D. \(69,2\% \).

Lời giải

Chọn D

Tổng số bi trong thùng là \(7 + 8 + 9 = 24\) (bi).

Số kết quả có thể khi lấy ra \(2\) viên bi bất kỳ từ \(24\) viên bi là \(C_{24}^2 = 276\).

Số kết quả thuận lợi khi lấy ra hai bi khác màu là \(C_7^1C_8^1 + C_8^1C_9^1 + C_9^1C_7^1 = 191\).

Gọi \(A\) là biến cố lấy ra hai viên bi khác màu\( \Rightarrow \)\(n\left( A \right) = 191\).

Xác suất xảy ra \(A\) là \(P\left( A \right) = \frac{{191}}{{276}} \simeq 69,2\% \).

A. \(\frac{{1881}}{{4060}}\).

B. \(\frac{{603}}{{812}}\).

C. \(\frac{{209}}{{812}}\).

D. \(\frac{{2179}}{{4060}}\).

Phương pháp

Áp dụng công thức tính xác suất

Lời giải

Chọn C

Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{30}^3\).

Gọi \(A\) là biến cố: “\(3\) đoàn viên được chọn có \(2\) nữ và \(1\) nam” thì \(n\left( A \right) = C_{11}^2.C_{19}^1\).

Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_{11}^2.C_{19}^1}}{{C_{30}^3}} = \frac{{209}}{{812}}\).

A. \(\frac{8}{{17}}\).

B. \(\frac{{25}}{{68}}\).

C. \(\frac{{25}}{{34}}\).

D. \(\frac{9}{{17}}\).

Phương pháp

Áp dụng công thức tính xác suất

Lời giải

Chọn A

Ta có: Số phần tử của không gian mẫu \(n\left( \Omega \right) = C_{17}^1.C_{16}^1\).

Gọi \(A\) là biến cố: “ Viên bi được lấy lần thứ \(2\) là bi xanh”.

Trường hợp 1: Lần \(1\) lấy viên đỏ, lần \(2\) lấy viên xanh: Có \(C_9^1.C_8^1\) cách chọn.

Trường hợp 2: Lần \(1\) lấy viên xanh, lần \(2\) lấy viên xanh: Có \(C_8^1.C_7^1\) cách chọn.

\( \Rightarrow \)\(n\left( A \right) = C_9^1.C_8^1 + C_8^1.C_7^1\).

Vậy \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_9^1.C_8^1 + C_8^1.C_7^1}}{{C_{17}^1.C_{16}^1}} = \frac{8}{{17}}\).

Câu 23. Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( {2\,;\,5} \right)\); \(B\left( {3\,;\,7} \right)\). Tìm tọa độ của véctơ \(\overrightarrow {AB} \).

A. \(\left( { – 1\,;\, – 2} \right)\).

B. \(\left( {1\,;\,2} \right)\).

C. \(\left( {5\,;\,12} \right)\).

D. \(\left( {2\,;\,1} \right)\).

Phương pháp

Với \(A({x_A};{y_A});B({x_B};{y_B})\) thì \(\overrightarrow {AB} = \left( {({x_B} – {x_A});({y_B} – {y_A})} \right)\)

Lời giải

Chọn B

Ta có: \(\overrightarrow {AB} = \left( {1\,;\,2} \right)\).

Câu 24. Trong mặt phẳng \(Oxy\), cho \(\vec a = \left( {2\,;\,6} \right)\); \(\vec b = \left( { – 1\,;\,3} \right)\). Tọa độ vectơ \(4\overrightarrow a – 3\overrightarrow b \) là:

A. \(\left( { – 11\,;\,15} \right)\).

B. \(\left( {15\,;\, – 11} \right)\).

C. \(\left( {15\,;\,11} \right)\).

D. \(\left( {11\,;\,15} \right)\).

Phương pháp

Trong mặt phẳng \(Oxy\), cho \(\vec a = \left( {{a_1}\,;\,{a_2}} \right)\); \(\vec b = \left( {{b_1}\,;\,{b_2}} \right)\). Tọa độ vectơ \(k\overrightarrow a + t\overrightarrow b = (k{a_1} + t{b_1};k{a_2} + t{b_2})\)

Lời giải

Chọn D

Ta có: \(\left\{ \begin{array}{l}\vec a = \left( {2\,;\,6} \right)\\\vec b = \left( { – 1\,;\,3} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}4\vec a = \left( {8\,;\,24} \right)\\3\vec b = \left( { – 3\,;\,9} \right)\end{array} \right. \Rightarrow 4\overrightarrow a – 3\vec b = \left( {11\,;\,15} \right)\).

A. \(E\left( { – \frac{1}{4}\,;\,\frac{{25}}{4}} \right)\).

B. \(E\left( { – \frac{1}{4}\,;\, – \frac{{25}}{4}} \right)\).

C. \(E\left( {\frac{1}{4}\,;\,\frac{{25}}{4}} \right)\).

D. \(E\left( {\frac{1}{4}\,;\, – \frac{{25}}{4}} \right)\).

Phương pháp

Sử dụng công thức tính tọa độ

Lời giải

Chọn A

Vì \(E\) trên đoạn \(AB\) và \(AE = 3EB\) suy ra \(\overrightarrow {AE} = 3\overrightarrow {EB} \).

Gọi \(E\left( {x;y} \right)\) khi đó \(\overrightarrow {AE} = \left( {x – 5\,;\,y – 4} \right)\); \(\overrightarrow {EB} = \left( { – 2 – x\,;\,7 – y} \right)\).

Do đó \(\left\{ \begin{array}{l}x – 5 = 3\left( { – 2 – x} \right)\\y – 4 = 3\left( {7 – y} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = – \frac{1}{4}\\y = \frac{{25}}{4}\end{array} \right.\).

Vậy \(E\left( { – \frac{1}{4}\,;\,\frac{{25}}{4}} \right)\).

Câu 26. Cho đường thẳng \(d:3x + 5y – 7 = 0\). Véc tơ nào sau đây là véctơ chỉ phương của \(d\)?

A. \(\overrightarrow u = \left( {3\,;\, – 5} \right)\).

B. \(\overrightarrow u = \left( {5\,;\,3} \right)\).

C. \(\overrightarrow u = \left( {5\,;\, – 3} \right)\).

D. \(\overrightarrow u = \left( {3\,;\,5} \right)\).

Phương pháp

Phương trình đường thẳng \(d:ax + by + c = 0\)có VTPT là \(\overrightarrow n = (a;b).\)

Lời giải

Chọn C

Đường thẳng \(d\) có một véctơ pháp tuyến là \(\overrightarrow n = \left( {3\,;\,5} \right)\) nên \(d\) có một véctơ chỉ phương là \(\overrightarrow u = \left( {5\,;\, – 3} \right)\).

A. \(x – y + 3 = 0\).

B. \(x + y – 9 = 0\).

C. \(x + 2y – 15 = 0\).

D. \(x – 2y = 0\).

Phương pháp

Phương trình đường thẳng \(d:a(x – {x_0}) + b(y – {y_0}) = 0\) có VTPT là \(\overrightarrow n = (a;b).\) đi qua điểm \(A({x_0},{y_0})\)

Lời giải

Chọn A

Gọi \(I\) là trung điểm của \(BC\)\( \Rightarrow \)\(I\left( {1\,;\,4} \right)\).

Ta có \(\overrightarrow {AI} = \left( { – 2\,;\, – 2} \right)\)\( \Rightarrow \)\(\overrightarrow n = \left( {1\,;\, – 1} \right)\) là vectơ pháp tuyến của đường thẳng \(AI\).

Phương trình đường thẳng \(AI\) là: \(1\left( {x – 3} \right) – 1\left( {y – 6} \right) = 0 \Leftrightarrow x – y + 3 = 0\)

Câu 28. Tìm các giá trị thực của tham số \(m\) để đường thẳng \(y = \left( {{m^2} – 6} \right)x + 2m + 5\) song song với đường thẳng \(y = 3x – 1\).

A. \(m = \pm 3\).

B. \(m = \pm 2\).

C. \(m = – 3\).

D. \(m = 3\).

Phương pháp

Để đường thẳng \(y = ax + b\) song song với đường thẳng \(y = a’x + b’\)thì \(\left\{ \begin{array}{l}a = a’\\b \ne b’\end{array} \right.\)

Lời giải

Chọn D

Để đường thẳng \(y = \left( {{m^2} – 6} \right)x + 2m + 5\) song song với đường thẳng \(y = 3x – 1\) thì điều kiện là

\(\left\{ \begin{array}{l}{m^2} – 6 = 3\\2m + 5 \ne – 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \pm 3\\m \ne – 3\end{array} \right. \Leftrightarrow m = 3\).

A. \(7\). B. \( – 3\). C. \(3\). D. \(7\).

Phương pháp

Khoảng cách từ điểm \(A({x_0},{y_0})\) đến đường thẳng \(d:ax + by + c = 0\) là \(d\left( {A,d} \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Lời giải

Chọn C

Ta có: \(M\left( {3\,;\,4} \right) \in d \Rightarrow 3 + 4b + c = 0 \Rightarrow c = – 3 – 4b\) \(\left( 1 \right)\).

\(d\left( {A,d} \right) = \frac{{\left| {2 + 5b + c} \right|}}{{\sqrt {1 + {b^2}} }} = \frac{{3\sqrt 5 }}{5} \Leftrightarrow 5{\left( {2 + 5b + c} \right)^2} = 9\left( {1 + {b^2}} \right)\) \(\left( 2 \right)\).

Thay \(c = – 3 – 4b\) vào \(\left( 2 \right)\) ta được:

\(5{\left( {b – 1} \right)^2} = 9\left( {1 + {b^2}} \right)\)\( \Leftrightarrow \).

\( \Rightarrow \)\(b = – 2\); \(c = 5\)\( \Rightarrow \)\(b + c = 3\).

Câu 30. Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} + {y^2} + 2\left( {m – 3} \right)x + 6my + 9m + 19 = 0\) là phương trình đường tròn.

A. \( – \frac{1}{2} < m < 2\).

B. \(m \frac{1}{2}\).

C. \(m 2\).

D. \(m 2\).

Phương pháp

Phương trình đường tròn có dạng \({x^2} + {y^2} – 2ax – 2by + c = 0\,\,\left( {{a^2} + {b^2} – c > 0} \right)\). và tọa độ tâm \(I(a,b)\), bán kính \(\,R = \sqrt {{a^2} + {b^2} – c} \)

Lời giải

Chọn D

Ta có \({x^2} + {y^2} + 2\left( {m – 3} \right)x + 6my + 9m + 19 = 0{\rm{ }}\left( 1 \right)\).

Phương trình \(\left( 1 \right)\) là phương trình đường tròn\( \Leftrightarrow \)\({\left( {m – 3} \right)^2} + {\left( {3m} \right)^2} – \left( {9m + 19} \right) > 0\)

\( \Leftrightarrow \)\(10{m^2} – 15m – 10 > 0\)\( \Leftrightarrow \)\(\left[ \begin{array}{l}m 2\end{array} \right.\).

Câu 31. Trong mặt phẳng \(Oxy\), đường tròn \(\left( C \right):{x^2} + {y^2} + 6x + 2y – 26 = 0\) có tâm là

A. \(I\left( { – 3\,;\, – 1} \right)\).

B. \(I\left( {3\,;\,1} \right)\).

C. \(I\left( {2\,;\,6} \right)\).

D. \(I\left( { – 2\,;\, – 6} \right)\).

Phương pháp

Lời giải

Chọn A

Ta có phương trình đường tròn là: \({\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} = 36\).

Vậy tâm đường tròn là: \(I\left( { – 3\,;\, – 1} \right)\).

A. \({\left( {x – 4} \right)^2} + {\left( {y – 4} \right)^2} = 16\).

B. \({\left( {x – 3} \right)^2} + {\left( {y – 3} \right)^2} = 9\).

C. \({\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} = 1\).

D. \({\left( {x – 2} \right)^2} + {\left( {y – 2} \right)^2} = 4\).

Phương pháp

Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x – a)^2} + {(y – b)^2} = {R^2}\)

Lời giải

Chọn D

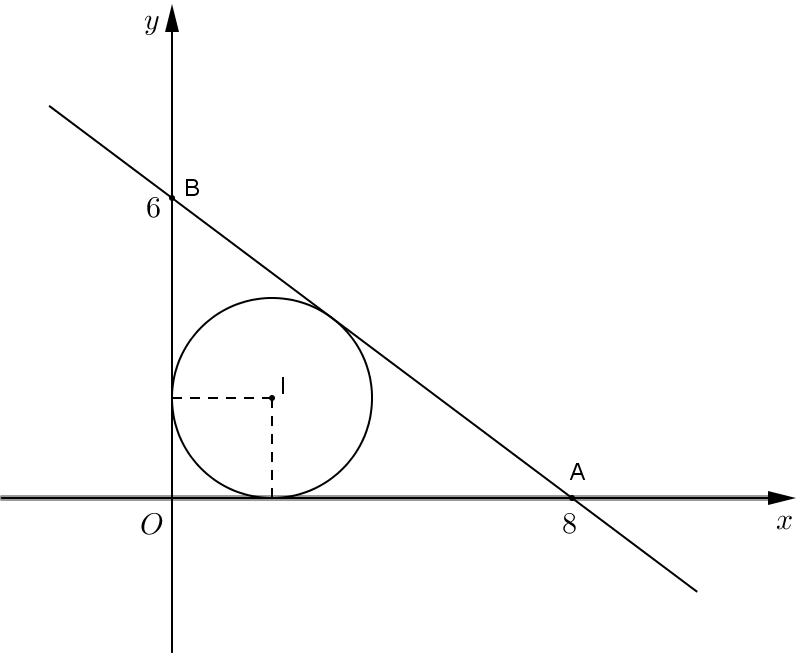
Phương trình đường thẳng \(AB\) theo đoạn chắn là: \(\frac{x}{8} + \frac{y}{6} = 1\) hay \(3x + 4y – 24 = 0\).

Ta có: \(d\left( {O;AB} \right) = \frac{{24}}{5}\).

Vì các điểm \(A\left( {8\,;\,0} \right)\) và \(B\left( {0\,;\,6} \right)\) nằm trong góc phần tư thứ nhất nên tam giác \(OAB\) cũng nằm trong góc phần tư thứ nhất. Do vậy gọi tâm đường tròn nội tiếp là \(I\left( {a\,;\,b} \right)\) thì \(0 < a < \frac{{24}}{5}\); \(0 < b < \frac{{24}}{5}\).

Theo đề ra ta có: \(d\left( {I;Ox} \right) = d\left( {I;Oy} \right) = d\left( {I;AB} \right)\).

Do vậy ta có: .

Vậy phương trình đường tròn cần tìm là: \({\left( {x – 2} \right)^2} + {\left( {y – 2} \right)^2} = 4\).

Câu 33. Cặp điểm nào là các tiêu điểm của elip \(\left( E \right)\): \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{5} = 1\)?

A. \({F_1} = \left( {0\,;\,2} \right)\); \({F_2} = \left( {0\,;\, – 2} \right)\).

B. \({F_1} = \left( {2\,;\,0} \right)\); \({F_2} = \left( { – 2\,;\,0} \right)\).

C. \({F_1} = \left( {3\,;\,0} \right)\); \({F_2} = \left( { – 3\,;\,0} \right)\).

D. \({F_1} = \left( {0\,;\,3} \right)\); \({F_2} = \left( {0\,;\, – 3} \right)\).

Phương pháp

Phương trình Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có hai tiêu điểm \({F_1} = \left( {c\,;\,0} \right)\); \({F_2} = \left( { – c\,;\,0} \right)\) với \(c = \sqrt {{a^2} – {b^2}} \)

Lời giải

Chọn B

Ta có: \({a^2} = 9\); \({b^2} = 5\)\( \Rightarrow \)\({c^2} = {a^2} – {b^2} = 4\)\( \Rightarrow \)\(c = 2\)\( \Rightarrow \)\({F_1} = \left( {2\,;\,0} \right)\); \({F_2} = \left( { – 2\,;\,0} \right)\).

A. \(T = \frac{2}{3}\). B. \(T = 1\). C. \(T = \frac{1}{3}\). D. \(T = \frac{3}{2}\).

Phương pháp

Diện tích hình tròn: \({S_T} = \pi .{R^2}\)với R là bán kính hình tròn, diện tích elip là \(S = \pi ab\) trong đó \(a\); \(b\) lần lượt là độ dài nửa trục lớn và nửa trục bé của elip.

Lời giải

Chọn B

Diện tích hình tròn: \({S_T} = \pi {.20^2}\), diện tích elip là \({S_E} = \pi .40.20\).

Tỷ số diện tích \(T = \frac{{{S_T}}}{{{S_E} – {S_T}}} = \frac{{\pi {{.20}^2}}}{{\pi .40.20 – \pi {{.20}^2}}} = 1\).

Câu 35. Cho elip . Tìm toạ độ điểm \(M \in \left( E \right)\) sao cho M nhìn \({F_1}{F_2}\) dưới một góc vuông:

Phương pháp

Điểm \(M\) nhìn \({F_1}{F_2}\) dưới một góc vuông khi và chỉ khi \({\left( {M{F_1}} \right)^2} + {\left( {M{F_2}} \right)^2} = {\left( {{F_1}{F_2}} \right)^2}\)

Lời giải

Chọn D

Ta có: \({a^2} = 36\); \({b^2} = 9\)\( \Rightarrow \)\({c^2} = {a^2} – {b^2} = 27\)\( \Rightarrow \)\(a = 6\); \(b = 3\); \(c = 3\sqrt 3 \).

\( \Rightarrow \)\(M{F_1} = 6 + \frac{{\sqrt 3 }}{2}x\); \(M{F_2} = 6 – \frac{{\sqrt 3 }}{2}x\).

\(M\) nhìn \({F_1}{F_2}\) dưới một góc vuông khi và chỉ khi \({\left( {M{F_1}} \right)^2} + {\left( {M{F_2}} \right)^2} = {\left( {{F_1}{F_2}} \right)^2}\).

\( \Leftrightarrow \)\({\left( {6 + \frac{{\sqrt 3 }}{2}x} \right)^2} + {\left( {6 – \frac{{\sqrt 3 }}{2}x} \right)^2} = 108\)\( \Leftrightarrow \)\(x = \pm 2\sqrt 6 \)\( \Rightarrow \)\(x = \pm \sqrt 3 \).

\( \Rightarrow \)\(M\left( {2\sqrt 6 \,;\,\sqrt 3 } \right)\); \(M\left( { – 2\sqrt 6 \,;\,\sqrt 3 } \right)\); \(M\left( {2\sqrt 6 \,;\, – \sqrt 3 } \right)\); \(M\left( { – 2\sqrt 6 \,;\, – \sqrt 3 } \right)\).

PHẦN TỰ LUẬN (3,0 điểm)

Bài 1. (1,0 điểm) Từ \(2\) chữ số \(1\) và \(9\) lập được bao nhiêu số tự nhiên có \(9\) chữ số sao cho không có \(2\) chữ số \(1\) đứng cạnh nhau?

Phương pháp

Sử dụng các quy tắc đếm

Lời giải

TH 1: Có \(9\) chữ số \(9\): Có \(1\) số.

TH 2: Có \(1\) chữ số \(1\); \(8\) chữ số \(9\): Có \(9\) cách xếp chữ số \(1\) nên có \(9\) số.

TH 3: Có \(2\) chữ số \(1\); \(7\) chữ số \(9\):

Xếp \(7\) chữ số \(9\) ta có \(1\) cách.

Từ \(7\) số \(9\) ta có có \(8\) chỗ trống để xếp \(2\) chữ số \(1\).

Suy ra có: \(C_8^2\) số.

TH 4: Có \(3\) chữ số \(1\); \(6\) chữ số \(9\):

Từ \(6\) chữ số \(9\) ta có \(7\) chỗ trống để xếp \(3\) chữ số \(1\).

Suy ra có: \(C_7^3\) số.

TH 5: Có \(4\) chữ số \(1\); \(5\) chữ số \(9\):

Từ \(5\) chữ số \(9\) ta có \(6\) chỗ trống để xếp \(4\) chữ số \(1\).

Suy ra có: \(C_6^4\) số.

TH 6: Có \(5\) chữ số \(1\); \(4\) chữ số \(9\): Có \(1\) số.

Vậy có: \(1 + 9 + C_8^2 + C_7^3 + C_6^4 + 1 = 89\) số thỏa mãn yêu cầu bài toán.

Bài 2. (0,5 điểm) Cho đa giác đều \(2023\) đỉnh. Hỏi có bao nhiêu tam giác có đỉnh là đỉnh của đa giác và có một góc lớn hơn \(120^\circ \)?

Phương pháp

Sử dụng các quy tắc đếm

Lời giải

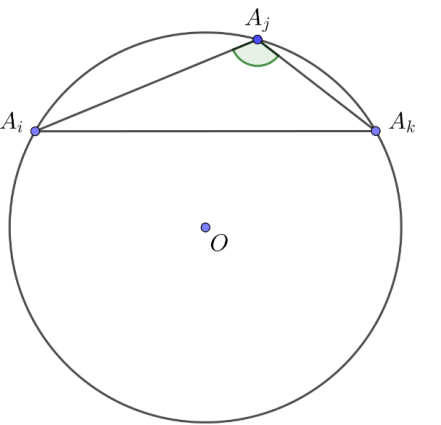
Gọi \({A_1}{A_2}…{A_{2023}}\) là các đỉnh của đa giác đều \(2023\) đỉnh.

Gọi \(\left( O \right)\) là đường tròn ngoại tiếp đa giác đều \({A_1}{A_2}…{A_{2023}}\). Các đỉnh của đa giác đều chia \(\left( O \right)\) thành \(2023\) cung tròn bằng nhau, mỗi cung tròn có số đo bằng \(\frac{{360^\circ }}{{2023}}\).

Vì tam giác cần đếm có đỉnh là đỉnh của đa giác nên các góc của tam giác là các góc nội tiếp của \(\left( O \right)\).

Suy ra góc lớn hơn \(120^\circ \) sẽ chắn cung có số đo lớn hơn \(240^\circ \). Cố định một đỉnh \({A_i}\). Có \(2023\) cách chọn \({A_i}\). Gọi \({A_i}\); \({A_j}\); \({A_k}\) là các đỉnh sắp thứ tự theo chiều kim đồng hồ sao cho cung nhỏ thì cung lớn \( \Rightarrow \)\(\widehat {{A_i}{A_j}{A_k}} > 120^\circ \) và tam giác \({A_i}{A_j}{A_k}\) là tam giác cần đếm.

Khi đó là hợp liên tiếp của nhiều nhất \(\left[ {\frac{{120}}{{\frac{{360}}{{2023}}}}} \right] = 674\) cung tròn nói trên.

\(674\) cung tròn này có \(675\) đỉnh. Trừ đi đỉnh \({A_i}\) thì còn \(674\) đỉnh. Do đó có \(C_{674}^2\) cách chọn hai đỉnh \({A_j}\);\({A_k}\). Vậy có tất cả \(2023C_{674}^2\) tam giác thỏa mãn yêu cầu bài toán.

Phương pháp

\(M\) là hình chiếu vuông góc của \(I\) xuống đường thẳng \(d\)với \(I\) là điểm sao cho \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \)

Lời giải

Gọi \(I\) là điểm sao cho \(\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \overrightarrow 0 \). Suy ra \(I\left( {1\,;\,3} \right)\).

Ta có: \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MI} + \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} \).

\(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = 3\left| {\overrightarrow {MI} } \right| = 3IM\).

Vậy \(\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|\) nhỏ nhất khí \(IM\) nhỏ nhất.

\( \Leftrightarrow \)\(M\) là hình chiếu vuông góc của \(I\) xuống đường thẳng \(d\).

Đường thẳng \(d’\) đi qua \(I\) và vuông góc với \(d\) có phương trình: \(3x + 2y – 9 = 0\).

\(M\) là giao điểm của \(d\) và \(d’\) nên \(M\) là nghiệm của hệ phương trinh:

\(\left\{ \begin{array}{l}2x – 3y + 20 = 0\\3x + 2y – 9 = 0\end{array} \right.\)\( \Leftrightarrow \)\(\left\{ \begin{array}{l}x = – 1\\y = 6\end{array} \right.\)\( \Rightarrow \)\(M\left( { – 1\,;\,6} \right)\).

Phương pháp

\(M\) là giao điểm của đoạn \(BP\) và đường tròn \(\left( C \right)\) với \(P\) là trung điểm \(IN\), \(N\) là giao điểm của đoạn \(IA\) và đường tròn \(\left( C \right)\), I là tâm đường tròn.

Lời giải

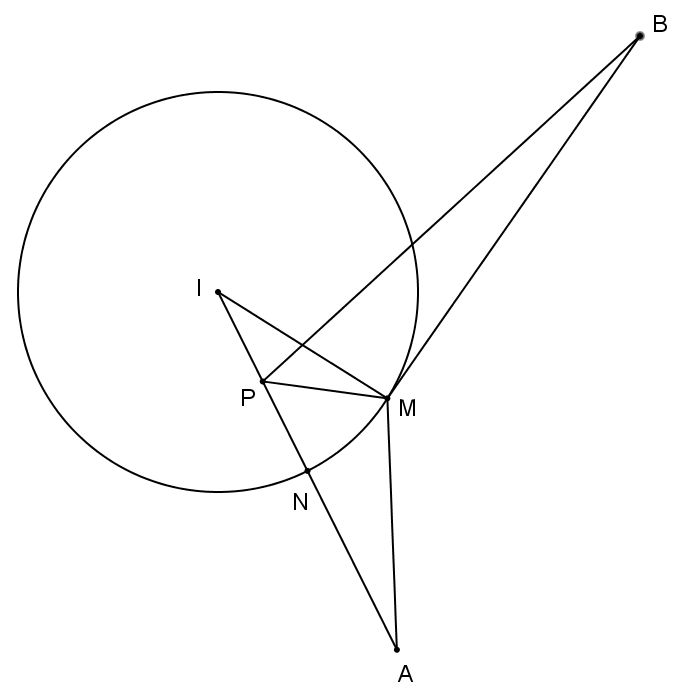
Đường tròn \(\left( C \right)\) có tâm \(I\left( {1\,;\,2} \right)\) bán kính \(R = 2\).

\(IA = 4 > R\); \(IB = 7 > R\) nên \(A\); \(B\) nằm ngoài đường tr